The history of infinitesimal geometry, and especially the part dealing with areas and volumes, surfaces and curved solids, is characterized by a particular aspect. After reaching the heights we know from Archimedes’ writings, research came to an abrupt halt for more than a millennium, only to resume in the ninth century with the Arab mathematicians. Over the course of two centuries, thanks to the latter, it reached other peaks before stopping again – no less decisively than in the third century BCE. A new revival occurred in the seventeenth century, and this time the research did not stop again. This is a historical phenomenon that has not been sufficiently emphasized, but which deserves analysis in order to clarify the reasons why research experienced these two beginnings and these two interruptions.
However, an anomaly never comes alone. The impact of Archimedes’ writings in this field, starting in the ninth century, appears under a somewhat paradoxical light. Very little of these writings was known in Arabic – just two treatises in all: On the Measurement of the Circle and On the Sphere and Cylinder. Yet, despite the small number of translated texts, a multiple and high-level research rapidly began. Due to how the Archimedean Corpus was preserved and transmitted, only a modest number of Archimedes’ works were known in Late Antiquity. In the sixth century, Eutocius seems to have known only the two cited above, and the situation in Arabic science was identical. All evidence indicates that the translators did not have the full Archimedean Corpus at their disposal, unlike the works of Euclid or Apollonius. We can even assert without fear of contradiction that Arab mathematicians knew only the two aforementioned treatises from Archimedes on infinitesimal mathematics. This conclusion is drawn from the examination of their works, and confirmed by the twelfth-century mathematician Ibn al-Sarīʾ. They were not aware of On the Quadrature of the Parabola, Conoids and Spheroids, The Spiral Lines, The Method, neither directly nor indirectly. This fact is important because the Archimedean method of integral sums that complemented the method of exhaustion is applied only in Conoids and Spheroids and The Spiral Lines – treatises that Arab mathematicians did not know. Nor were Archimedes’ methods for determining the area of a parabolic sector or the volume of a paraboloid sector known to them.
The question thus reduces to discovering how these two treatises were received in the Arabic tradition – and this will be important in identifying the aspects that characterise the Arab mathematicians belonging to the Archimedean tradition. Meanwhile, those who received and studied them were engaged in research on conic sections; some time later, at least from the Banū Mūsā onwards, they had Apollonius’ Conics at their disposal. These mathematicians were also interested in disciplines that today might be called ‘applied’: astronomy, statics, mechanics and optics. From this interest emerged the development of research on the conics: their optical properties; plotting point by point through geometric transformation; continuous plotting by specially constructed instruments; and research on projective methods. We therefore expect from them the introduction of other methods in addition to those of Archimedes, or the strengthening of techniques used by him but in a fragmentary way. Indeed, these mathematicians, engaged in the study of point transformations and projections, would combine such methods with infinitesimal techniques. They were also aware of the work of their algebraist colleagues, which in some way influenced their research in infinitesimal geometry. We are in the presence of a body of knowledge that would imprint on the concepts and methods of the Arabic authors of the Archimedean tradition and determine the development of research in infinitesimal geometry. We therefore expect to see them not only deepen the understanding of asymptotic behaviours and infinitesimal objects, but also extend the field of research to include sectors of infinitesimal geometry not explicitly treated by the Syracusan mathematician: isoperimetric problems in the plane and in space, solid angle, lunes. It becomes clear, therefore, that these Archimedeans are not, like Eutocius, commentators of Archimedes, but his emulators. Moreover, the number of commentaries and Arabic editions of the two Archimedean treatises on infinitesimal geometry is extremely limited: as far as we know, there are only those by al-Kindī on On the Measurement of the Circle, by al-Māhānī on On the Sphere and Cylinder, and by Nāṣir al-Dīn al-Ṭūsī on both treatises. Let us now briefly and systematically consider the various sectors of this infinitesimal geometry in the mathematics of the classical Islamic period.
The first known Arabic text on Archimedean problems is a commentary by the philosopher and mathematician al-Kindī on the third proposition (approximation of π) of On the Measurement of the Circle, entitled Risālat al-Kindī ilā Yūḥannā ibn Māsawayh fī taqrīb al-dawr min al-watar (Epistle of al-Kindī to Yūḥannā ibn Māsawayh on the Approximation of the Ratio of the Circumference to the Diameter), written before 856. Already in this work, the impact of algebra can be seen. Al-Kindī uses algebraic vocabulary for certain terms and to express ratios between numbers and segments – ratios that no ancient Greek would have admitted. This commentary would also become known in Latin, as suggested by the famous ‘Florence Versions.’ The true renewal of research on Archimedean problems begins with three contemporaries of al-Kindī, the brothers Muḥammad, Aḥmad, and al-Ḥasan, all known as the Banū Mūsā. They are the authors of the celebrated Kitāb Maʿrifat misāḥat al-ashkāl al-basīṭa wa-ʾl-kuriyya (Book on the Measurement of Plane and Spherical Figures), the first work by Arab Archimedeans. Let us focus on this book, which dates from the time of the reception of Archimedes’ work.
A simple glance suffices to understand that it is indeed a book that fits into the Archimedean tradition, yet without taking On the Sphere and Cylinder as a model. In fact, the authors do not follow Archimedes’ approach, even though some fundamental ideas remain the same. In this treatise of eighteen propositions, they address four topics: the measurement of the circle, that of the surface and volume of the sphere, Hero of Alexandria’s formula for the area of a triangle, and, finally, the issue of the two mean proportionals and the trisection of the angle. At the end of the treatise, the Banū Mūsā assess their contribution, writing: “Everything we have described in our book is our own work, except the knowledge of the circumference from the diameter, which is due to Archimedes, and the knowledge of the position of two magnitudes between two others so that [all four] follow the same ratio, which is due to Menelaus, as we mentioned before” (Rashed 1996a, p. 132).
This statement, usually overlooked, instead deserves reflection. Let us briefly return to the study of the Banū Mūsā to understand the meaning of their declaration and at the same time their precise position in the Archimedean tradition. They begin by demonstrating the following proposition: given a circle of circumference $p$ and a segment of length $l$, two cases are possible: if $l < p$, one can inscribe in the circle a polygon of $n$ sides with perimeter $p_n$ such that $l < p_n < p$; if $l > p$, one can circumscribe about the circle a polygon of $n$ sides with perimeter $q_n$ such that $p < q_n < l$. The demonstration of the two cases rests on the existence of a circle of given circumference $p$ and a regular polygon. The authors assume that such a circle exists; for the polygon they rely on Prop. 16 of Book XII of Euclid’s Elements: “Given two circles with the same center, inscribe in the larger circle an equilateral polygon, having an even number of sides, that does not touch the smaller circle.”

Note that for a regular $n$-gon to satisfy the problem, it is necessary and sufficient that its apothem $a_n$ meets the condition:
\begin{equation} r_1 < a_n < r_2 \Leftrightarrow r_1 < r_2 \cos \frac{\pi}{n} < r_2 \Leftrightarrow \frac{p_1}{p_2} < \cos \frac{\pi}{n} < 1\ \text{,} \end{equation}where $r_1$ and $r_2$ are the radii of the two concentric circles, $p_1$ and $p_2$ their respective circumferences (the existence of the integer $n$ depends on the continuity of the cosine function). However, contrary to what has been asserted, reference to the cited proposition from the Elements is not enough to establish the Banū Mūsā’s proposition; it must be completed by a homothety, a technique known to al-Ḥasan ibn Mūsā.
In the next proposition, the Banū Mūsā prove by contradiction the expression for the area of a circle as the product of the semidiameter by the semicircumference, i.e., $S = r p /2$. Note that to obtain a contradiction they do not compare $S$ with $S’ > S$, nor $S$ with $S’’ < S$, but only $p$ with $p’ > p$ and $p$ with $p’’ < p$, thus comparing lengths.
After thus determining the area of the circle, they turn to the approximation of π using Archimedes’ method, as they themselves affirm, but with some slight modifications. It is evident that the approach of the Banū Mūsā, as outlined above, differs from that of Archimedes in several respects. The first difference concerns precisely the application of the method of exhaustion and of its complementary technique, reductio ad absurdum. We have seen how, contrary to Archimedes, the Banū Mūsā bypass the most delicate point of the method of exhaustion – namely, the passage to the limit (to use our terminology) – by resorting to Prop. 16 of Book XII of the Elements, plus a homothety, a proposition whose demonstration is itself obtained precisely by passing to the limit. As for the reductio ad absurdum, we have seen that they compare lengths, not areas as Archimedes did. Finally, they do not determine the area of the circle by comparison with another figure, that of the right triangle in which one leg equals the radius and the other the circumference, but directly, as the product of two magnitudes. Under these conditions, one understands how their demonstration is shorter than that of Archimedes.
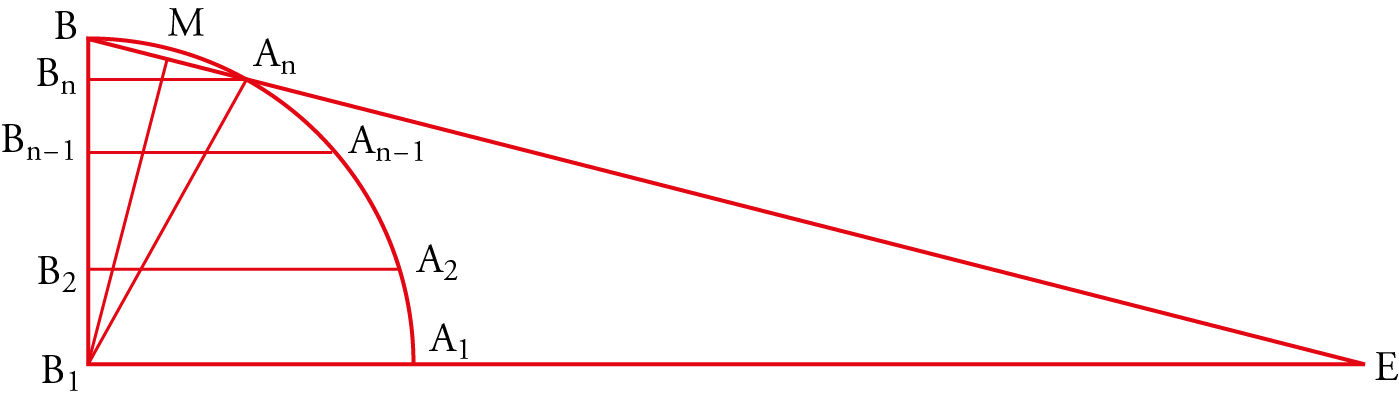
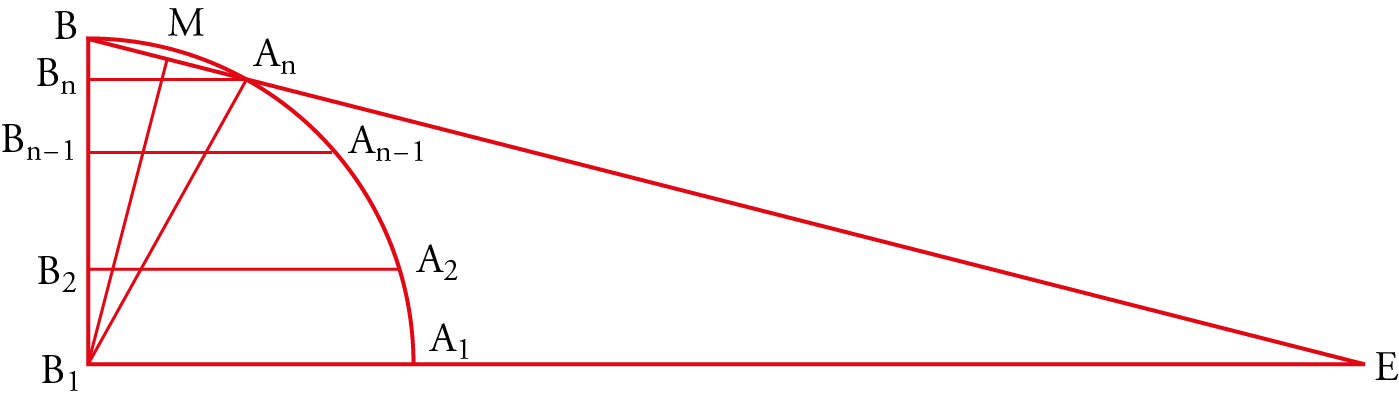
It remains to discover whether the path followed by the Banū Mūsā was chosen deliberately or was imposed by circumstances. To answer this, one must have an idea of the study they conducted on the second topic: the measurement of the surface area and the volume of the sphere. They begin by proving the following proposition (Prop. 11): the lateral surface area of a truncated cone of revolution with parallel bases is given by $S=l(p_1+p_2)/2$, where $l$ is the length of the slant height and $p_1, p_2$ are the perimeters of the two bases. Proposition 12 states that if one divides the quarter of a circle $A_1B$ into $n$ equal arcs by the points $A_2, A_3,\cdots, A_n$, then:
\begin{equation} A_1B_1 + 2\sum_{k=1}^n A_k B_k -B_1E \end{equation} \begin{equation} B_1 M^2< \frac{\ 1\ }{2}\ BA_n(B_1A_1 + 2\sum_{k=1}^n B_k A_k) < B_1B^2 \ \text{.} \end{equation}After computation, [2] and [3] become:
\begin{equation} 2\sum_{k=1}^n \sin k\cdot \frac{\pi}{2n} = \coth{\frac{\pi}{4n}}+1 \end{equation} \begin{equation} \cos^2{\frac{\pi}{4n}}<\cos{\frac{\pi}{4n}}<1 \end{equation}These relations are satisfied for every $n$.
In Proposition 13, they consider a semicircle in which a regular polygonal line with an even number of sides is inscribed. Within it, they draw the inscribed semicircle. By rotation, a hemisphere and a solid of revolution are generated, composed of a cone and various truncated cones, along with another hemisphere inscribed within the solid of revolution and sharing the same center as the first. The Banū Mūsā demonstrate that $2\pi R_1^2 < S < 2\pi R_2^2$, where $R_1$ and $R_2$ are the radii of the inscribed and circumscribed circles, respectively. We observe that the assumptions are those of Proposition 12, and that the demonstration uses Propositions 11 and 12, without employing Prop. 16 of Book XII of the Elements.
They are now able to apply reductio ad absurdum twice: first in Proposition 14 to obtain the lateral surface area of a hemisphere, which is twice that of a great circle, as they say, namely $S=2\pi R^2$; and second, to deduce the volume of the sphere as the product of the semidiameter by one third of the surface area, that is, $(4/3)\pi R^3$.
Here again we find the differences between Archimedes and the Banū Mūsā already noted in the case of the measurement of the circle. The first again concerns the method of exhaustion. This time too, the Banū Mūsā apply Prop. 16 of Book XII of the Elements, together with a homothety, and not Prop. 17 of the same book as has been believed. In fact, they consider a solid inscribed within the hemisphere composed of cones and truncated cones, whose surface lies outside that of a concentric hemisphere contained within the first. Such a solid is obtained from a regular polygonal line inscribed in a great circle of the sphere and not touching the great circle of the second sphere contained within the first (thus again starting from the cited Prop. 16 of Euclid). This procedure allows them to avoid the passage to the limit with the series of sines already mentioned. On the other hand, even here, when it comes to determining the volume of the sphere, the reductio ad absurdum is applied to the lateral surfaces and not to the volumes. Finally, the volume of the sphere is not given, as in Archimedes, in terms of another volume (a cone having as base a great circle of the sphere and as height the radius), but as the product of two magnitudes.
This study by the Banū Mūsā had important effects on mathematics, albeit of varying nature. First of all, in the Arab world, this initial phase – which would be quickly surpassed – had a certain impact on research, but above all on teaching. Beginning with their collaborator Thābit ibn Qurra, and for a century and a half, the study of the measurement of curved surfaces and volumes continued. This tradition rediscovered the method of integral sums, while developing geometric methods to facilitate the application of the method of exhaustion, such as affinity. The measurement of the sphere would later be revisited by Ibn al-Haytham, who used Darboux sums. In the Arabic tradition, the treatise of the Banū Mūsā would survive primarily as a teaching text, as demonstrated by the large number of copies found in manuscript collections, evidently intended for this purpose. In Latin, the situation is entirely different. Translated by Gerard of Cremona, the treatise, together with Archimedes’ On the Measurement of the Circle (translated into Latin from the Arabic version), became the main reference work in Archimedean mathematical research. Among many others, Fibonacci, Jordanus de Nemore, the anonymous author of the Liber de triangulis, and Roger Bacon showed interest in this treatise.
We have noted that modern commentators on this treatise, albeit in excellent works, have been misled in believing that the Banū Mūsā relied solely on Prop. 16 of Book XII of Euclid and especially in claiming that they used the subsequent Prop. 17. This oversight stems from the failure to recognize the explicit use of geometric transformations (homothety), since the contribution of the Banū Mūsā has been examined in light of the old geometry. One need only consult the book by al-Ḥasan ibn Mūsā on the ellipse, entitled Kitāb al-shakl al-mudawwar al-mustatīl (Book on the Elongated Circular Figure), to understand the growing importance in geometry of the study of geometric transformations. It is precisely in this direction that Arabic geometry would increasingly depart from its Greek and Hellenistic origins. This is a fundamental thesis for us, and it requires, among other things, rewriting the history of geometry in that era.
To highlight only what concerns us here, from the very beginning it is observed that the Archimedean tradition in Arabic, in developing an infinitesimal geometry, tends to orient geometric research toward the study of pointwise transformations. The history of this tradition thus appears in a new light, and the position of the Banū Mūsā is redefined. We now turn to this second book, which is, in our view, essential for understanding the first. Al-Ḥasan ibn Mūsā sets out to determine the area of the ellipse and of elliptical sections. We know that he did not yet have an intelligible version of Apollonius’s Conics. His research also aimed to develop the study of conic sections starting from the plane sections of the cylinder. It was only after his death that his brother Aḥmad ibn Mūsā found Eutocius’s edition of the first four books of the Conics, making possible the Arabic translation of the entire seven-book work of Apollonius (the eighth having already been lost in Greek).
In other words, al-Ḥasan ibn Mūsā sought to achieve two objectives: one, so to speak, Archimedean, concerning the measurement of an area bounded by a curve; the other, in the tradition of Apollonius (even if he could not fully know the Conics), concerning the study of the geometric properties of curves. He combines the notions of projection and orthogonal affinity with the application of Prop. 2 of Book XII of the Elements and reductio ad absurdum: it is the first change of direction in Archimedean mathematics.
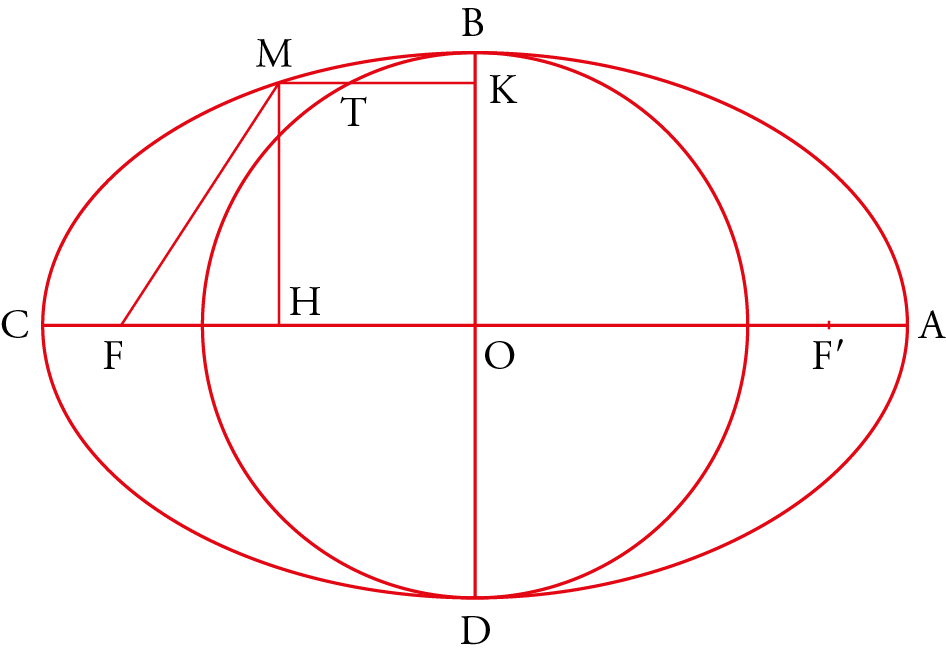
Following Ibn al-Samḥ’s book, which summarizes al-Ḥasan ibn Mūsā’s treatise, the latter’s procedure unfolds as follows: he begins with the “elongated circular figure” (fig. 4) defined by the bifocal property $MF+MF’=2a$, where $2a$ is the major axis, to then establish that the plane section of a cylinder of revolution by a non-base-parallel plane – i.e., an ellipse – shares the same properties as the first figure. He then determines the axis of the ellipse and finally studies the properties of chords, arrows, and so forth.
The outline of his deductive reasoning shows that the first six propositions concern the elongated circular figure – its vertices, center, diameters, chords, axis, the inscribed circle having the minor axis as diameter, and the circumscribed circle having the major axis as diameter. The next five propositions concern the ellipse as a plane section and its identification with the previous curve. Then follows a group of eight propositions dealing with the measurement of the area of the ellipse. Let us consider these groups in summary.
In the penultimate proposition of the first group (Prop. 5), one reads: if one associates to a point M of the elongated circular figure the point $T$ of the inscribed circle having the same ordinate ($MT$ is orthogonal to $BD$ at point $K$), it holds that: $MK^2=KT^2 + ¼(OA^2-MF^2)^2$ which, in the coordinate system $y=MK, y=MH$, with $AC=2a, BD=2b, F_1F_2=2c, KT=X$, and $MF=a-(cx/a)$ (relation previously established), can be rewritten as
\begin{equation} x^2-\frac{c^2}{a^2}\ x^2+y^2=b^2 \end{equation}(dividing by $b^2$ yields the equation of the ellipse). Prop. 6 concerns the orthogonal affinity relative to the minor axis:
\begin{equation} \frac{MK}{TK}=\frac{OA}{OB}\Leftrightarrow \left[\frac{x}{X}=\frac{a}{b}\right] \text{;} \end{equation}from this, and from the previous equation, one obtains:
\begin{equation} x^2\left(1 - \frac{c^2}{a^2} \right) = X^2 = b^2 - y^2 \Leftrightarrow b^2 x^2 = a^2 X^2 \text{,} \end{equation}which yields:
\begin{equation} \frac{x}{X}=\frac{a}{b}\ \text{,} \end{equation}an orthogonal affinity with axis $BD$, ratio $a/b>1$, in which the elongated circular figure $ABCD$ is the image of the circle of diameter $BD$ (this affinity is a dilation).

In the second group of propositions, devoted to the ellipse as a plane section of the right cylinder, al-Ḥasan ibn Mūsā, after recalling the property that the section of a right circular cylinder by a plane cutting the axis and not parallel to the base is an ellipse with center on the axis, considers a family of curves that deform continuously from the circle to the ellipse. He then studies the orthogonal affinity relative to the minor axis (Prop. 7): let an ellipse $ADBG$ and an inscribed circle $EDZG$ (fig. 5) be given; if a line parallel to $AB$ intersects $GD$ at $H$, the circle at $K$, and the ellipse at $T$, then:
\begin{equation} \frac{HT}{HK}=\frac{AB}{GD}=\frac{a}{b}\ \text{.} \end{equation}In the course of the demonstration, he considers the ellipse $ADBG$ as the flipped version of the ellipse $DLG$ obtained by rotating $ADBG$ around $DG$ on the plane perpendicular at $N$ to the axis of the cylinder. The circle $DEG$ is the cylindrical projection of the ellipse $DLG$ onto this same plane.
In Prop. 8 he studies the orthogonal affinity relative to the major axis. The ellipse is considered in this case as the image of the circumscribed circle in an orthogonal affinity of ratio $a/b$ (a contraction). In other terms, and in analytic language unknown to al-Ḥasan ibn Mūsā, if in an orthogonal reference the ellipse $ \mathscr{E}$ and the circles $ \mathscr{C}_1$ and $ \mathscr{C}_2$ are defined as follows $a>b$
\begin{align} \mathscr{E}=\left[(x,y)\ , \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\right]\ ,\notag\\ \mathscr{C}_1=\left[(X,Y)\ , X^2+Y^2=b^2\right]\ ,\notag\\ \mathscr{C}_2=\left[(X,Y)\ , X^2+Y^2=a^2\right]\ \text{;} \end{align}and if $\psi$ and $\varphi$ denote the dilation and contraction already seen, then:
\begin{align} \mathscr{E}=\psi(\mathscr{C}_1)\ ,\quad\text{with}\ \psi\ :\ (X,Y)\rightarrow(x.y)\ :\begin{cases}x=\frac{a}{b}\ X\\y=Y\ ,\end{cases}\notag\\ \mathscr{E}=\varphi(\mathscr{C}_2)\ ,\quad\text{with}\ \varphi\ :\ (X,Y)\rightarrow(x.y)\ :\begin{cases}x=X\\ y=\frac{b}{a}\ Y\ . \end{cases} \end{align}At this point, he demonstrates that the two figures, the elongated circle and the ellipse, are superposable point by point (Prop. 9). These are the conceptual tools he then uses to determine the area of the ellipse. First, he shows by means of a dilation that the ratio between the area of a polygon inscribed in the ellipse and that of a polygon inscribed in the circle inscribed in the ellipse is equal to the ratio between the major and minor axes. He then specifies these results to obtain π ab as the area of the ellipse.
This, in brief, is the method of al-Ḥasan ibn Mūsā, a path that sheds light both on the earlier book of the Banū Mūsā and on the results of their Archimedean heirs. The use of a homothety in the book of the Banū Mūsā is entirely natural; the recourse to pointwise transformations by their successors, such as Thābit ibn Qurra, his grandson Ibrāhīm ibn Sinān, and many others, originates with the Banū Mūsā themselves. Their profile is thus transformed: no longer a pale reflection of Archimedes’ commentators, but rather mathematicians who, in order to inaugurate a new tradition, begin by revisiting the old one. Their heirs, mathematicians of genius, would soon go even further, thereby paradoxically veiling their importance and role. Historians of mathematics have addressed this by attributing to their successors – especially Thābit ibn Qurra – some of their inventions, conflating two aspects that are in fact quite distinct: that which was transmitted by Latin mathematics and that which is found in Arabic mathematics.
As we have seen, at the very moment when two texts by Archimedes were being translated, the mathematicians of the 9th century were seeking their own paths to achieve the same results, or others entirely new. This quest for new paths is not limited among the Banū Mūsā and their successors to Archimedean teaching, but also appears in their work in mechanics and astronomy. Indeed, the same tendency can be observed in other mathematical disciplines: arithmetic, number theory, algebra, trigonometry, projective methods, etc., and in other scientific fields such as optics with al-Kindī and statics with Thābit ibn Qurra. This new scientific spirit that took shape in the 9th century – within the tradition of Hellenistic science but with great freedom from it, the freedom to invent, to critique, and to draw from other sources, such as Indian sources – explains at least in part a phenomenon that continues to surprise: the massive, repeated, and ever faster translation of the ancient heritage.
The contemporaries and heirs of the Banū Mūsā would very actively continue research in this field. One of their collaborators, Thābit ibn Qurra (826-901), would make a substantial contribution. He would write three treatises: one devoted to the area of a parabolic segment, a second to the volume of a paraboloid of revolution, and the third to the sections and lateral area of the cylinder. These works would serve as new points of departure for other mathematicians, who aimed to reduce the number of lemmas and to improve the methods. The measurement of the parabola would be taken up again, for example, by al-Māhānī, by Ibrāhīm ibn Sinān, and by Ibn Sahl, while that of the paraboloid would be further developed by al-Qūhī and later by Ibn al-Haytham. All this demonstrates the foundational role played by the writings of Thābit ibn Qurra in this topic, as in many others.
In the first treatise, Kitāb fī misāḥat qiṭʿ al-maʿrūj alladhī yusammā al-mukāfiʾ (Book on the Measurement of the Segment of a Cone Called Parabola), in which he aims to determine the area of a parabolic segment, Thābit ibn Qurra – who was unaware of Archimedes’ study on the subject – proves twenty-one results. The first ones concern the sum of various arithmetic progressions; for example, he demonstrates that:
\begin{align} 2\sum_{k=1}^nk^2= \frac{\ 1\ }{2}\sum_{k=1}^n(2k-1)^2+n^2+\frac{n}{2}\ \text{;} \notag\\\sum_{k=1}^n(2k-1)^2=\frac{4n^3}{3}-\frac{n}{3}\ \text{;}\cdots \end{align}After eleven arithmetic lemmas, he states four lemmas concerning sequences of segments, which he uses to study bounding arguments. In Lemma 14 he proves that: if $a$ and $b$ are two segments with a known ratio $a/b$, then there exists a positive integer n such that the sequence $(u_k)_{1\le k\le n}$ of the first $n$ odd numbers starting from 1, and the sequence $(v_k)_{1\le k\le n}$ of the first $n$ even numbers starting from 2, satisfy the following relation:
\begin{equation} \frac{n}{v_n\cdot\displaystyle\sum_{k=1}^nu_k}<\frac{a}{b} \end{equation}With this result, he introduces an approximation which he uses in the next lemma to achieve the subdivision of segments. The lemma states: let $AB$ and $H$ be two segments, and let $a$ and $b$ be two segments with a given ratio $a/b$. For any $n$, one has: (a) there exists a partition $(A_k)_{0\le k\le n}$, $k = 0, 1, …, n$, with $A_0=A$, $A_n =B$, such that
\begin{equation} \frac{A_k\ A_{k+1}}{A_{k+1}\ A_{k+2}}=\frac{u_{k+1}}{u_{k+2}}\quad \text{for}\quad\ 0\le k\le n-2\ \text{,} \end{equation}where $(u_k)_{1\le k\le n}$ is the sequence of odd numbers starting from 1; (b) there exists a sequence of segments $(H_j)_{1\le j\le n}$, $j=1, 2, \cdots, n$, with $H_n=H$, such that
\begin{equation} \frac{H_j}{H_{j+1}}=\frac{v_j}{v_{j+1}}\quad \text{for}\quad\ 1\le j\le n-1\ \text{,} \end{equation}with $(v_j)_{1\le j\le n}$ the sequence of even numbers starting from 2. If $n$ satisfies the earlier relation (14), then:
\begin{equation} \frac{n\ A_0\ A_1\cdot \displaystyle\frac{H_1}{2}}{AB\cdot H}< \frac{a}{b} \ \text{.} \end{equation}The proof rests on the subdivision of a given segment into a sequence of segments proportional to a given sequence, and on the generalization of Lemma 14, which introduces the approximation of segment sequences and thus the generalization of the upper bound of a sequence of segment ratios.
After the fifteen lemmas – eleven arithmetic and four related to sequences of segments – Thābit ibn Qurra tackles the calculation of the area of a parabolic segment. To this end, he proves four propositions. The examination of the lemmas and these propositions shows that he had a precise and rigorous understanding of the concept of the least upper bound (supremum) of a sequence of squares of real numbers and of its uniqueness. To characterize the supremum, he uses the following property.
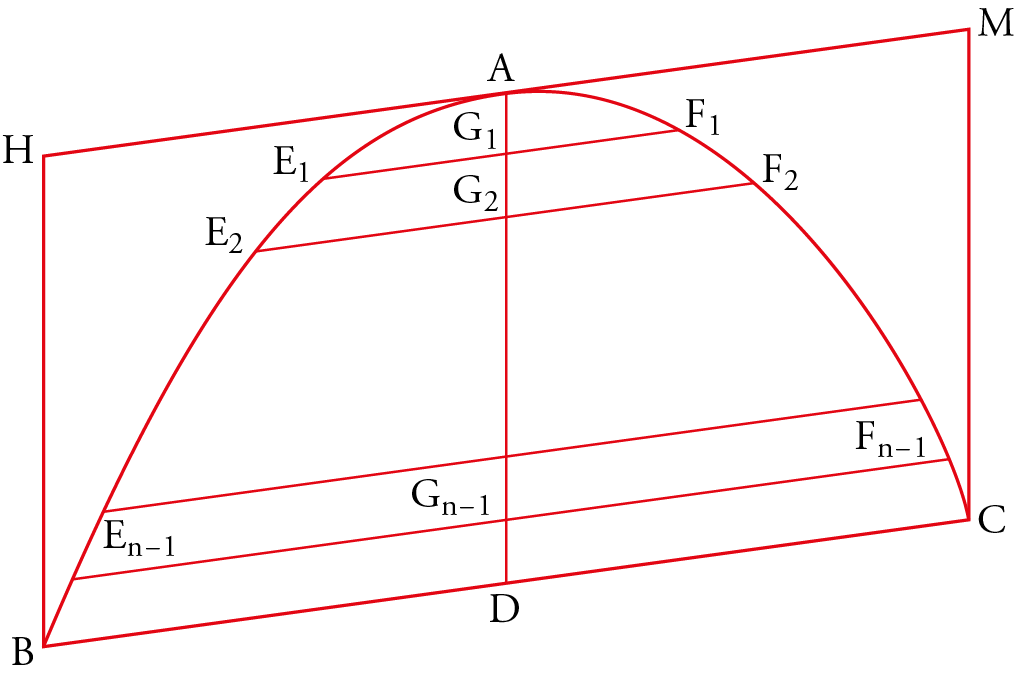
Let $BAC$ be a parabolic segment with diameter $AD$, and let $S$ be the area of the parallelogram with base $BC$ associated with the parabola. Then, for every$\epsilon>0$, there exists a subdivision $A$, $G_1, G_2, \cdots, G_{n-1}, D$ of the diameter $AD$ such that the difference between the area of $BAC$ and the area of the polygon $BE_{n-1} \cdots E_2E_1AF_1F_2\cdots F_{n-1}C$ is less than $\epsilon$. He rigorously proves that the least upper bound of the areas of the polygons obtained is 2/3 of the area of $BHMC$, and he finally arrives at the following theorem: the area of the parabola is infinite, but the area of any segment is equal to 2/3 of the area of the parallelogram associated with the segment.
Let $\mathscr {S}$ be the area of the parabolic segment $\mathscr {P}$ and $\mathscr {S}$ the area of the associated parallelogram. If $(2/3)S \ne \mathscr {S}$, two cases arise. In the first case, $\mathscr {S}>(2/3)S$. Let $\epsilon >0$ such that
\begin{equation} \mathscr{S}-\frac{\ 2\ }{3}\ S=\epsilon \ \text{.} \end{equation}By Prop. 18, for this $\epsilon$ there exists $N$ such that, for $n>N$, the polygon $\mathscr {P}_n$ of the area $S_n$ satisfies:
\begin{equation} \mathscr{S}- S_n<\epsilon \ . \end{equation}From the above (18) and (19), $\lbrack (2/3)S+\epsilon\rbrack S_n$, so $(2/3)S < S_n $. But by Prop. 17, $(2/3) S > S_n$, which is a contradiction. In the second case, $\mathscr{S}< (2/3)S $. Let $\epsilon > 0$ such that
\begin{equation} \frac{\ 2\ }{3}\ S- \mathscr{S}=\epsilon \text{.} \end{equation}By Prop. 19, for this $\epsilon$ there exists $N$ such that, for $n>N$, the polygon $\mathscr {P}_n$ of area $S_n$ satisfies:
\begin{equation} \frac{\ 2\ }{3}\ S- S_n<\epsilon \ . \end{equation}Hence, by (20) and (21), \( [ \mathscr{S} + \epsilon ] - S_n < \epsilon \), or \( \mathscr{S} < S_n \). But \( \mathscr{P}_n \) is inscribed in \( \mathscr{P} \). This gives a contradiction. Hence, \( \frac{2}{3} S = \mathscr{S} \).
This theorem is equivalent to demonstrating the uniqueness of the least upper bound and essentially relies on the properties of the supremum. Indeed, we wish to demonstrate that $(2/3)S=\mathscr{S}$, knowing that:
\begin{equation} \mathscr{S}=\text{sup}(S_n)_{\scriptscriptstyle n\scriptscriptstyle\ge\scriptscriptstyle1} \end{equation} \begin{equation} \frac{\ 2\ }{3}\ S=\text{sup}(S_n)_{\scriptscriptstyle n\scriptscriptstyle\ge\scriptscriptstyle1} \end{equation}
By reductio ad absurdum, assume $\mathscr{S}\ne(2/3)S$. Two cases arise. In the first, if $\mathscr{S}> (2/3)S$, then there exists $\epsilon>0$ such that $\mathscr{S}= (2/3)S+\epsilon$. But since $\mathscr{S}$ is the least upper bound of the $S_n$, there exists an $S_n$ such that $S_n>\mathscr{S}-\epsilon$, so $(2/3)S < S_n$ – a contradiction, since $(2/3)S$ is also an upper bound of the $S_n$.
In the second case, if \( \mathscr{S} < \frac{2}{3} S \), then there exists \( \epsilon > 0 \) such that \( \frac{2}{3} S = \mathscr{S} + \epsilon \). But \( \frac{2}{3} S \) is the least upper bound of the \( S_n \), so there exists \( S_n \) such that \( S_n > \frac{2}{3} S - \epsilon \), hence \( \mathscr{S} < S_n \); absurd, since by (22) \( \mathscr{S} \) is an upper bound of the \( S_n \).
We do not claim that Thābit ibn Qurra, any more than his predecessors or successors until the 18th century, defined the concept of least upper bound. However, it does appear that he used the properties of the supremum as a guiding idea in the measurement of convex sets. In Ibn Qurra’s procedure one can in fact recognize the fundamental idea underlying the Riemann integral. Indeed, in the special case where the considered diameter is the axis of the parabola, the procedure is equivalent to considering a subdivision $\sigma = AG_1G_2\cdots G_{n-1}$ of the diameter $AD$, taking the sum
\begin{equation} S_{\sigma}=\sum_{i=1}^n(AG_i-AG_{i-1})\ \frac{G_{i-1}F_{i-1}+G_iF_i}{2} \end{equation}and proving that, for every $\epsilon >0$, there exists a subdivision s such that the difference between the area $ACD$ and $S_{\sigma}$ is less than $\epsilon$, and finally proving that $S_{\sigma}$ converges to this area.
Translating the above into the language of analysis: let $x_i$ be the abscissa of $G_i$ and let $y = f(x)$ be the equation of the parabola. $S_{\sigma}$ can then be written as:
\begin{equation} S_{\sigma}=\sum_{i=1}^n(x_i-x_{i-1})\ \frac{f(x_{i-1}f_{i-1}+f(x_i)}{2}\ ; \end{equation}but since
\begin{equation} f(x_{i-1})\le\ \frac{f(x_{i-1})+f(x_i)}{2}\ \le f(x_i)\ ; \end{equation}is a value assumed by $f$ at some point $x_i$ in the interval $[x_{i-1}, x_i]$, and since $f$ is continuous, it follows that
\begin{equation} \frac{f(x_{i-1})+f(x_i)}{2} \end{equation}is a value that $f$ takes at the point $\xi_i$ in the interval $x_{i-1}, x_i$. But $S_{\sigma}$ can then be written in the form
\begin{equation} S_{\sigma}=\sum_{i=1}^n(x_i-x_{i-1})\ f(\xi _i)\ ;\quad x_{i-1}\le \xi_i \le x_i \ \text{,} \end{equation}which is precisely the sum used in the definition of the Riemann integral of a function $f$. Lastly, observe that Ibn Qurra’s quadrature, given the definition of the parabola, is equivalent to calculating the integral $\int_0^a \sqrt{px}\, dx$. As the modern historian Adolf P. Youschkevitch wrote:
“Thanks to this procedure, Ibn Qurra revives the method of calculating integral sums, which had fallen into oblivion. Moreover, with this very method, Ibn Qurra effectively calculates for the first time an integral $\int_0^a x^n\, dx$ for a fractional exponent $n$, here $\int_0^a x^{1/2}\, dx$. In doing so, again for the first time, he subdivides the interval of integration into unequal parts. With a similar procedure, which consists in subdividing the x-axis into segments forming a geometric series, Pierre Fermat, in the mid-17th century, would address the quadrature of curves $y=x^{m/n}$ with $(m,\,n) \ne 1$.” (1976, p. 43)
After calculating the area of the parabola, Ṯābit ibn Qurra addresses the volume of a paraboloid of revolution in his Maqāla fī misāḥat al-mujassamāt al-mukāfiʾa (Treatise on the measurement of paraboloids). This involves a transition from plane geometry to solid geometry, and for this purpose he establishes thirty-six propositions divided into various groups. He ultimately demonstrates the following theorem: the volume v of a parabolic dome $ABC$ with axis $BD$ is half the volume $V$ of the cylinder with height $h$ and circular base with diameter $AC$:
\begin{equation} v= \frac{\ 1\ }{2}\ V=\frac{\ 1\ }{2}\ \pi h\ \frac{AC^2}{4}\ \text{.} \end{equation}The procedure is analogous to that used for determining the area of a parabolic sector. It involves dividing the diameter of a parabolic sector into segments proportional to the sequence of odd numbers. The points on the parabola corresponding to this division then have abscissas proportional to the squares of integers and ordinates proportional to the integers themselves. These points determine:
| in the plane | in space |
|---|---|
| 1. a polygon inscribed in the parabola and decomposed into trapezoids | 1. a solid of revolution inscribed in the paraboloid and decomposed into cone-like solids |
| 2. Let $s$, be the area of the parabola | 2. Let $v$, the volume of the paraboloid |
| 3. $S$, the area of the associated parallelogram | 3. $V$, the volume of the associated cylinder |
| 4. $s_i$, the area of a trapezoid | 4. $v_i$, the volume of a cone-like solid |
He shows that, given $\epsilon>0$, one can find an $N$ such that for all $n>N$, the following holds:
\begin{align} &\frac{2}{3}S-\sum_{i=1}^ns_i<\epsilon\ \text{(props. 17, 19)} && \frac{V}{2}-\sum_{i=1}^nv_i<\epsilon\ \text{(props. 32, 35)} \notag \\ &s-\sum_{i=1}^ns_i<\epsilon\ \text{(prop. 18)} && v- \sum_{i=1}^nv_i<\epsilon\ \text{(props. 33, 34)} \end{align}In other words, he demonstrates:
\begin{align} &\frac{2}{3}S=\text{sup}\sum_{i=1}^ns_i && \frac{V}{2}=\text{sup}\sum_{i=1}^nv_i \notag \\ &s=\text{sup}\sum_{i=1}^ns_i && v=\text{sup}\sum_{i=1}^nv_i \end{align}Through reductio ad absurdum, he proves the uniqueness of the supremum in both cases:
\begin{align} &s=\frac{2}{3}\ S\ \text{(prop. 20)}&& v=\frac{V}{2}\ \text{(prop. 36)} \end{align}Ṯābit ibn Qurra’s contributions in this field extend further. He composed a fundamental book, Kitāb fī quṭūʿ al-usṭuwāna wa-basīṭihā (Book on the sections of the cylinder and its lateral surface), in which he studies the various plane sections of a right and an oblique cylinder, determines the area of the ellipse and its sectors, discusses maximal and minimal cylinder sections and their axes, and finally determines the area of the lateral surface portion bounded by two plane sections. Like the previous two treatises, this one not only left a mark on the history of infinitesimal geometry, but is also one of the most important texts in all of geometry. Indeed, by addressing the study of geometric pointwise transformations, it directs geometric research in a new direction and in doing so fertilizes algebra. Traces of this influence are found in the works of, among others, Ibrāhīm ibn Sinān, Ibn Sahl, al-Qūhī, Ibn al-Haytham, and Sharaf al-Dīn al-Ṭūsī.
It is impossible to report here all the results and demonstrations of this rich and profound treatise. To fix ideas, let us mention just two propositions. In prop. 14, Ṯābit shows that if $S$ is the area of the ellipse $\mathscr{E}$ with semi-axes $a$ and $b$, and $\Sigma$ is the area of the circle $E$ with radius $r=\sqrt{ab}$, then $S=\Sigma$. The symbolic translation of his demonstration uses the following notation: $S$, area of the ellipse $\mathscr{E}$; $S_n$, area of $P_n$ inscribed in $\mathscr{E}$; $\Sigma$, area of the equivalent circle $E$; $\Sigma_n$, area of $\Pi_n$ inscribed in E; $S’$, area of the circumscribed circle $\mathscr{C}$; $S’_n$, area of $P’_n$ inscribed in $\mathscr{C}$. Suppose $S\ne\Sigma$. There are two cases. First, if $S>\Sigma$, then $S=\Sigma+\epsilon$. Let $P_n$ be a $2_{n+1}$-gon inscribed in $\mathscr{E}$, derived from $P_{n-1}$ by doubling its vertices through diametric cuts. $P_1$ is the rhombus defined by the ellipse’s vertices. If $S_n$ is the area of $P_n$, then successively:
\begin{align} &S_1>\frac{\ 1\ }{2}S\Rightarrow S-S_1< \frac{\ 1\ }{2} S \notag \\ &S_2-S_1>\frac{\ 1\ }{2} (S-S_1)\Rightarrow S-S_2<\frac{\ 1\ }{2^2} S \notag \\ &\cdots \notag \\ & S_n-S_{n-1}>\frac{\ 1\ }{2} (S-S_{n-1})\Rightarrow S-S_n< \frac{\ 1\ }{2^n}S \end{align}then, for $\epsilon$ given by $S=\Sigma+\epsilon$, there exists a positive integer $n$ such that $(1+2^n)S<\epsilon$, implying $S-S_n<\epsilon$ and $S_n>\Sigma$. Now consider the circle $\mathscr{C}$ and polygon $P’_n$ derived from $\mathscr{C}$ and $P_n$ via an orthogonal affinity with ratio $a/b$. Let $S’_n$ be the area of $P’_n$ and $S’$ the area of $\mathscr{C}$. We then have:
\begin{equation} \frac{S_n}{S'_n}=\frac{b}{a}=\frac{ab}{a^2}=\frac{\Sigma}{S'}\ \text{;} \end{equation}but since $S_n>\Sigma$ , it follows $S’_n>S’$, which is impossible. In the second case, if $S<\Sigma$ we similarly obtain a contradiction:
\begin{equation} \frac{\Sigma}{S'}=\frac{S}{S'-\epsilon'} \ \text{.} \end{equation}By taking again the circle $\mathscr{C}$ and the previous polygons $P’_n$, one obtains successively:
\begin{align} &S'-S'_1<\frac{\ 1\ }{2}\ S' \notag \\ &S'-S'_2<\frac{\ 1\ }{2^2}\ S' \notag \\ &\cdots \notag \\ &S'-S'_n<\frac{\ 1\ }{2^n}\ S'\ \text{;} \end{align}Then, for $\epsilon’$ defined as in (35), there exists a positive integer $n$ such that $(1/2^n)S’<\epsilon’$, hence:
\begin{equation} S'-S'_n<\epsilon' \ \text{.} \end{equation}If $P_n$ is the polygon inscribed in $\mathscr{E}$ corresponding to $P’_n$ under the orthogonal affinity of ratio $b/a$, then:
\begin{equation} \frac{S_n}{S'_n}=\frac{\Sigma}{S'}=\frac{S}{S'-\epsilon'}\ \text{.} \end{equation}But from (37), it follows that $S’_n>S’-\epsilon’$, which is absurd. After examining both cases, one therefore concludes $S=\Sigma$.
We pass from the ellipse $\mathscr{E}$ to the circle $\mathscr{C}$ with an orthogonal dilation $f$ of ratio $k_1 = a/b$, and from the circle $\mathscr{C}$ of radius $a$ to the circle $E$ of radius $r$ such that $r^2=ab$, with a homothety $h$ of ratio $k_2=r/a=\sqrt{ab}/a=\sqrt{b/a}$. Thus, $E=h\circ f(\mathscr{E})$; the transformation $h\circ f$ preserves area, since $K_1\cdot k^2_2 =1$. The aim of prop. 14 is precisely to demonstrate this property for the ellipse $\mathscr{E}$.
Using the previous notation, Thābit employs the equalities $\Sigma/S’=b/a=k^2_2$, and shows that $S_n/S’_n=b/a=1/k_1$ for every $n$, from which:
\begin{equation} S=\Sigma\Leftrightarrow\frac{S}{S'}=\frac{\Sigma}{S'}\Leftrightarrow\frac{S}{S'}=\frac{S_n}{S'_n}\ \text{.} \end{equation}His method consists of two steps. In the first, assuming $S_n / S’_n < S / S’$ , we get:
\begin{equation} \frac{S_n}{S'_n}=\frac{S-\epsilon_1}{S'}\ \text{.} \end{equation}One shows that there exists \( P_n \subset \mathscr{E} \) such that \( S^{\prime}-\epsilon_1 < S^{\prime}_n < S^{\prime} \); but \( f(P_n) = P^{\prime}_n \subset \mathscr{E} \) satisfies (40), from which \( S^{\prime}_n > S^{\prime} \), which is impossible.
In the second step, assuming $S_n/S’_n > S/S’$, we get:
\begin{equation} \frac{S_n}{S'_n}=\frac{S}{S'-\epsilon_2}\ \text{.} \end{equation}One shows that there exists \( P'_n \subset \mathscr{E} \) such that \( S^{\prime} - \epsilon_2 < S^{\prime}_n < S^{\prime} \); but \( f^{-1}(P'_n) = P_n \subset \mathscr{E} \) satisfies (41), from which \( S_n > S \), which is impossible. Thus, it is demonstrated that:
\begin{equation} \frac{S}{S'}=\frac{S_n}{S'_n}\ \text{.} \end{equation}
Hence, starting from the property of orthogonal affinity whereby the ratio of the areas$S’_n$ and $S_n$ of the two homologous polygons $P_n$ and $P’_n$ is equal to the affinity ratio $a/b$, for any $n$, Thābit deduces that the same holds for the area $S$ of the ellipse $\mathscr{E}$ and the area $S’$ of the circle $\mathscr{C}$. This amounts to saying that the ratio is preserved in the passage to the limit:
\begin{equation} \frac{S_n}{S'_n}=\frac{b}{a}\quad\text{and}\quad\frac{S}{S'}=\frac{\text{lim}\ S_n}{\text{lim}\ S'_n}=\text{lim}\ \frac{S_n}{S'_n}=\frac{b}{a}\ \text{.} \end{equation}Luca Valerio (1552-1618) will take such statements as the basis for his method (De centro gravitatis solidorum libri tres, Book II, props. I–III), a method which does not involve integral sums.
The same result is found in prop. 4 of Archimedes’ Conoids and Spheroids, a text that was unknown to the mathematicians of the time, including c. The comparison between Archimedes’ method and Thābit’s is doubly instructive: it enhances our appreciation of the ninth-century mathematician's contribution and helps us better understand the extent of knowledge about the Archimedean corpus in that era.
In Proposition 31, Thābit demonstrates that the lateral area $\Sigma$ of a portion of an oblique cylinder bounded between two right sections is $\Sigma=pl$, where $p$ is the length of a minimal ellipse and $l$ the length of the generating segment between the two sections. Let $\mathscr{E}$ be one of the sections, $K$ its center, and $2a$ the major axis. Let us distinguish again two cases.
In the first case, if \( \Sigma < pl \), there exists \( g \), with \( g < p \), such that \( \Sigma = gl \). Let \( h \) be such that \( g < h < p \); there exists an area \( \epsilon \) such that \( \Sigma + \epsilon = hl \), hence \( \epsilon = l(h - g) \). One constructs the ellipse \( \mathscr{E}_1 = \varphi(\mathscr{E}) \), where \( \varphi \) is the homothety centered at \( K \) with ratio \( a_1 / a \) such that \( 1 > a_1 / a > h / p \); by Proposition 26, the length \( p_1 \) satisfies \( p_1 / p = a_1 / a \), from which \( p_1 / p > h / p \), and thus \( p_1 > h \).
Let $P_n$ be a polygon inscribed in $\mathscr{E}$ and not touching $\mathscr{E}_1$, $P’_n$ its projection onto the other base, and $p_n$ the perimeter. If $\Sigma_n$ is the lateral area of the prism with bases $P_n$ and $P’_n$, then $\Sigma_n=p_n l$; but $p_n>p_1>h$, from which $\Sigma_n>hl$, and thus:
\begin{equation} \Sigma_n=\Sigma+\epsilon \ \text{.} \end{equation}a) If $\epsilon/2\ge s$, since the areas $s$ and $s′$ of the two bases—which are minimal ellipses—are equal, one has $\epsilon \ge s+s’$, from which $\Sigma_n>\Sigma+s+s’$. The lateral area of the prism inscribed in the cylinder would be greater than the total area, which is absurd.
b) If $\epsilon/2< s$, then a condition is imposed on $a_1$, namely $a_1^2/a^2>[s+(\epsilon/2)]/2$; but if $s_1$ is the area of $\mathscr{E}_1$, then $s_1/s=a_1^2/a^2$, from which $s-s_1<\epsilon/2$. If $s_n$ is the area of $P_n$ and $s’_n$ that of $P’_n$, one has $S_n=s’_n$, $s>s_n>s_1$, $s-s_n<\epsilon/2$ and $\epsilon>(s-s_n)+(s’-s’_n)$. From (44) one obtains $\Sigma_n>\Sigma+(s-s_n)+(s’-s’_n)$, which is absurd. From both (a) and (b) a contradiction is reached; therefore $\Sigma\ge pl$.
Let us now consider the second case: if $\Sigma>pl$, there exists $g$, with $g>pg$, such that $\Sigma=gl$. Let $h$ be such that $p
If \( p_1 \) is the length of \( \mathscr{E}_1 \), then \( \frac{p_1}{p} = \frac{a_1}{a} \), from which it follows that \( p_1 < h \). Inscribe in \( \mathscr{E}_1 \) a polygon \( P_n \) having no points in common with \( \mathscr{E} \); using the same notations as in the first part, we have \( \Sigma_n = p_n l \); but since \( h > p_1 > p_n \), it follows that \( \Sigma_n < hl \), and therefore:
However, since \( s_1/s = a_1^2 / a^2 \), then \( s_1 < s + (\epsilon / 2) \); that is \( s_1 - s > s_n - s \), from which \( s_n - s < \epsilon / 2 \). By convexity we know that \( \Sigma_n + (s_n - s) + (s^{\prime}_n - s^{\prime}) > \Sigma \), hence \( \Sigma_n + \epsilon > \Sigma \), contradicting (46). After examining both cases, one concludes therefore that \( \Sigma = pl \).
We observe that the only surface areas considered up to that time were those of the right cylinder, the right cone, and the sphere (Archimedes, On the Sphere and the Cylinder). Thābit is the first to study the area of the oblique cylinder, which will be expressed in modern mathematics by an elliptic integral (the length $p$ of the base ellipse). This proposition marks a step towards determining the lateral area of a portion of an oblique cylinder bounded between two planes, whether parallel or not. This is precisely what Thābit establishes in the following propositions.
With the contributions of the Banū Mūsā and Thābit ibn Qurra, research in infinitesimal geometry rested on solid foundations and had made notable progress. These mathematicians provided important experiences from which a new beginning could emerge: the era of the heirs begins. These experiences are not limited to the theorems demonstrated – although they are numerous – but also include new methods and the rediscovery of older ones. We have seen the development of two types of methods. Already with al-Ḥasan ibn Mūsā and his brothers Muḥammad and Aḥmad, and with Thābit ibn Qurra in his last treatise, we have observed the emergence of methods based on geometric transformations.
On the other hand, we have seen that Thābit ibn Qurra reintroduces the concept of integral summation, certainly already present in Archimedes but absent in the treatises translated into Arabic. However, a thorough study of the two Archimedean texts translated into Arabic – On the Measurement of the Circle and On the Sphere and Cylinder – could have put a mathematician of Thābit ibn Qurra’s caliber on the path to this rediscovery. Furthermore, his integral summations are more general than those of Archimedes: the intervals he takes in the subdivisions are not necessarily equal. In his study of the paraboloid, where he also proceeds by integral summations, he does not consider cylinders of equal height, as Archimedes did, but rather a cone and frustums of cones whose heights are in the ratio of successive odd natural numbers (starting from 1). It was therefore foreseeable that in the following period, during which mathematical research intensified and developed rapidly, mathematicians would seek to improve their predecessors' demonstrations and to develop both the methods of integral summation and of geometric transformations.
The first to advance in this direction was al-Māhānī (d. ca. 880). He resumed the measurement of the parabola to provide a much shorter demonstration than that of Thābit ibn Qurra. Unfortunately, al-Māhānī’s text is unavailable – though it may still exist – so we cannot form a precise idea of it. The second heir was the grandson of Thābit ibn Qurra, Ibrāhīm ibn Sinān (296-335/908-946). A brilliant mathematician with a brief life, he stated that he could not accept that al-Māhānī “had conducted a more advanced study than that of my grandfather without any of us surpassing him.” He thus sought to provide a shorter demonstration not only than that of his grandfather, which, as we have said, required twenty lemmas, but also than that of al-Māhānī.
Ibrāhīm ibn Sinān therefore wrote the Kitāb fī misāḥat al-qiṭāʿ al-mukāfiʾ (On the Measurement of the Parabola), a brief treatise particularly concise and elegant. The central idea of his text, which he is keen to demonstrate from the outset, is that an affine transformation preserves the proportionality of areas. With that, only two lemmas and a single proposition are needed to complete the study.
then the following proportionality holds between the areas of triangles and the areas of polygons:
In the proof, he uses the transformation $T$ defined in the statement. This is an affine transformation, and he demonstrates that it preserves the ratio of areas in both the case of triangles and of polygons.
The second lemma reads as follows: the ratio between the areas of two parabolic segments is equal to the ratio between the areas of their associated triangles. In it, Ibn Sinān demonstrates that an affine transformation preserves the ratio between the area of a parabolic segment and that of an associated triangle, as well as the ratio between their homologous elements. The underlying property is, in fact, the invariance of area ratios (even for curvilinear figures) under affine transformations. To this end, he uses Archimedes’ axiom to demonstrate that it is possible to inscribe in a parabolic segment a polygon whose area differs, by as little as desired, from that of the parabola.
Once this is established, calculating the ratio between the area of a parabolic segment and its associated triangle no longer requires infinitesimal procedures, but only the observation that this ratio does not depend on the specific segment considered. This is precisely what he demonstrates in the following proposition: the area of a parabolic segment is equal to 4/3 the area of its associated triangle. Ibn Sinān’s strategy for improving his grandfather’s demonstration and reducing the number of propositions from twenty to three relies on the combination of affine transformations and infinitesimal methods.
Al-Qūhī (second half of the 10th century) also reduces the 36 propositions established by Thābit ibn Qurra for calculating the volume of a paraboloid of revolution to three. However, while Ibn Sinān follows the geometric approach – the method of transformations – present in Thābit ibn Qurra’s work, al-Qūhī follows the other path, also present in Thābit’s work, which leads him to rediscover the integral summations found in the works of Archimedes that were unknown to Arabic mathematicians.
For the paraboloid of revolution, Archimedes considered cylinders of equal height, whereas Thābit ibn Qurra used adjacent frustums of cones, whose bases create a subdivision of the parabola’s diameter that generates the paraboloid. The segments of this subdivision are proportional to the odd natural numbers starting from 1, and the heights correspond to the segments in this subdivision. Al-Qūhī, in his effort to reduce the number of propositions demonstrated by Thābit, independently rediscovered integral summations as they appear in Archimedes. His method, in fact, differs from Archimedes’ only in a few details, particularly when demonstrating that the difference between inscribed and circumscribed cylinders can be made arbitrarily small. Here are the statements of his three propositions.
Proposition 1 is as follows. Given a paraboloid with axis $XF$ (fig. 12) and any subdivision with points of abscissa $(b_i)_{0 \le i \le n}$ and $b_0=0$, $b_n=XF$, let $(I_i)_{2 \le i \le n}$ be the volumes of the inscribed cylinders and $(C_i)_{1 \le i \le n}$ the volumes of the circumscribed cylinders associated with this subdivision, and let $V$ be the volume of the cylinder associated with the paraboloid. For all positive integers $n$, the following inequality holds:
Proposition 2 is as follows. Given a segment of a paraboloid between two arbitrary ordered surfaces, let $I$ and $C$ be the volumes of the inscribed and circumscribed cylinders, respectively. If this segment is cut by a surface equidistant from the two previous ones, we obtain two inscribed cylinders with volumes $I_1$ and $I_2$, and two homologous circumscribed cylinders with volumes $C_1$ and $C_2$. Then:
where $C-I$ is the volume of the ring $HGEC$, $C_1 - I_1$ the volume of the ring $NLMC$, and $C_2 - I_2$ the volume of the ring $LKGS$ (fig. 13). The proof of this proposition is as follows: starting with the subdivision of axis $XF$ with points of abscissa $(b_i)_{0 \le i \le n}$, with $(I_i)_{1 \le i \le n}$, $(C_i)_{1 \le i \le n}$, and $I_1 = 0$ as the volumes of the homologous cylinders, and then considering the sequence $(c_j)_{0 \le j \le 2n}$, with $c_0 = b_0$, $c_{2n} = b_n$, and $c_{2i+1} = (b_i + b_{i+1})/2$, and $(I^{\prime}_j)_{1 \le j \le 2n}$, $(C^{\prime}_j)_{1 \le j \le 2n}$ the volumes of the corresponding homologous cylinders associated with this new subdivision, the following relation holds:
In the third proposition, it is shown that if $P$ is the volume of a portion of a paraboloid and $V$ that of the associated cylinder, then $P = V/2$. Denoting by $(I_i^q)_{1 \le i \le n \cdot 2^q}$ and $(C_i^q)_{1 \le i \le n \cdot 2^q}$ the volumes of the cylinders associated with the subdivision, it follows from the previous proposition that:
for fixed $n$ and any positive integer $q$. This allows al-Qūhī, thanks to an extension of Proposition 1 from Book X of Euclid’s Elements, to assert that from a certain number of operations onwards:
or, in other terms, he shows that for every $\epsilon>0$, there exists an $N$ such that for every $q>N$, inequality (53) holds. But then:
and therefore:
Now, if $P = (V/2) + \epsilon$, it follows that $V/2 < \sum_{i=1}^{n \cdot 2^q} I_i^q$, which is impossible by Proposition 1. If instead $P = (V/2) - \epsilon$, one reasons similarly, since:
which implies:
and again, this is impossible in light of Proposition 1. Hence, we must conclude that $P=V/2$.
Al-Qūhī’s demonstration is quite swift, thanks to Proposition 1, which directly compares the sums of inscribed and circumscribed cylinders to the volume of the large cylinder, without needing to compute these sums explicitly, as Archimedes does by reducing the calculation to an arithmetic progression. The proof of this proposition is based on the inequalities $u_i - u_{i-1} < 2C_i$ and $u_i - u_{i-1} > 2I_i$, obtained by considering generic cylinders like $QGHR$ and $SBCO$ (fig. 12), which are neither inscribed nor circumscribed and thus are not given a priori.
Proposition 2 establishes that if the subdivision is refined by halving each interval, the excess of circumscribed over inscribed cylinders is halved. It plays the same role as Proposition 19 of Archimedes’ On Conoids and Spheroids.
Al-Qūhī’s method, through its use of integral summations, resembles that of Archimedes, though the application is somewhat different. It is as if al-Qūhī had independently rediscovered the use of integral sums.
Building upon the work of the Banū Mūsā and especially Thābit ibn Qurra, Ibn Sīnān follows a line of research that effectively combines geometric transformations and infinitesimal techniques, while al-Qūhī independently rediscovers, with the improvements we have seen, the methods of integral summation. In doing so, they not only offer their successors a new research perspective in infinitesimal geometry but also provide them with additional tools. These successors will not hesitate to revisit the problems addressed by their predecessors, adding new ones in the process.
The first to take this path appears to have been Ibn Sahl. He returned once again to the quadrature of the parabola; unfortunately, his treatise is still lost. However, based on his prominence among the mathematicians of the time, the various contributions we have reconstructed, and his familiarity with the work of al-Qūhī, we can surmise that he employed integral summation. This conjecture seems quite plausible not only for the reasons mentioned but also because Ibn al-Haytham (d. after 1040), his successor, revisits the measurement of the sphere and the paraboloid without referencing that of the parabola – as if that task had already been accomplished using the same method. It would fall to Ibn al-Haytham to bring this tradition, initiated a century and a half earlier, to its peak. With him, as we shall see, the calculation of curved surfaces and volumes reaches a level comparable to that found in other regions at the dawn of the seventeenth century.
He revisits the proof of the volume of the paraboloid of revolution, but he does not stop there: he also determines the volume of the paraboloid generated by the rotation of a parabola around an ordinate. Furthermore, he applies the same method to calculate the volume of the sphere. Before briefly presenting his method, we must recall a fundamental aspect of this mathematician's work, who was also a physicist and astronomer. While his predecessors, such as al-Qūhī, addressed the problem of infinitesimal determinations for curved surfaces and volumes – and while they also returned to the question of the center of gravity of such figures – Ibn al-Haytham would engage with the full spectrum of problems raised in this field: infinitesimal determinations, centers of gravity, isoperimetric problems, and solid angles. He also devoted attention to another topic, at least indirectly related to these: the study of lunes. Furthermore, in the course of these investigations and others, he encountered genuine differential problems. It is as if he intended to traverse the majority of the regions that would later constitute the continent of analysis.
Ibn al-Haytham’s treatise Maqāla fī misāḥat al-mujassam al-mukāfiʾ (On the Measurement of the Paraboloid) is structurally simple yet significant. In the introduction, in which he references the work of his predecessors Thābit ibn Qurra and al-Qūhī, he criticizes the former for “having followed a path lacking in structure and having limited his explanations to a long and laborious process” (p. 208), and the latter simply for having written a treatise that “contains only the proof for the measurement of one type of paraboloid” (ibid.). This introduction, which frames the work, is followed by an initial section devoted entirely to the arithmetic lemmas required for the demonstrations. He then addresses the sections on the paraboloid of revolution and the second type of paraboloid, concluding with a discussion of the method applied in this chapter.
He begins by demonstrating a general rule, via finite recurrence, for the calculation of the sums of the first $n$ integers raised to an arbitrary power iii. The rule is expressed as:
which allows him to establish an inequality necessary for the entire procedure:
The proof of this lemma is exceedingly long, yet it demonstrates both the depth of arithmetic investigation in this field and his mathematical virtuosity.
Ibn al-Haytham then proceeds to determine the volume of the paraboloid of revolution. He considers three cases, depending on whether the angle $\angle ACB$ is right, acute, or obtuse. Let us examine the first case in detail, following the author's process. If $V$ is the volume of the circumscribed cylinder and $v$ that of the paraboloid, the goal is to prove that $v = V/2$. Proceeding by contradiction, let us first suppose that $v > V/2$, i.e., $v - (V/2) = \epsilon$. Let $M$ be the midpoint of segment $AC$, and let line $MU$, parallel to $BC$, intersect the parabola at $E$ and line $BH$ at $U$. Let line $SEO^{\prime}$, parallel to $AC$, intersect $BC$ at $O^{\prime}$ and $AH$ at $S$. Denoting by $[EC]$ the solid generated by the rotation of surface $MCO^{\prime}E$, and analogously for the other solids, we have:
By iterating the construction from point $L$, the midpoint of $AM$, and then from point $K$, the midpoint of $MC$, we obtain:
therefore,
By iterating the construction at points $O$, $P$, $N$, and $J$ – the midpoints of segments $AL$, $LM$, $MK$, and $KC$ respectively – the sum of the eight solids will be equal to half of expression (62), that is, $\frac{\ 1\ }{8}V$. The procedure continues in the same fashion, that is, by subtracting solids of type (60) and (62) from the circumscribed cylinder. We thereby successively remove from $V$:
After a finite number of steps, we necessarily arrive at a remainder less than $\epsilon$, according to Lemma 1 of Book X of Euclid’s Elements (or Ibn al-Haytham’s theorem).
Let us suppose that the subdivision of the figure corresponds to the point at which the remainder is smaller than $\epsilon$. Let $V_n$ be the volume of the solids remaining after n$n$ steps; then $V_n < \epsilon$, and let $v_nv$ be the volume of the portion of these solids contained within the paraboloid. We have $v_n < V_n$ and thus $v_n < \epsilon$; by hypothesis, $v-v_n > \frac{\ 1\ }{2}V$. But by the properties of the parabola, we know:
which yields $CB^2 = 2EM^2$. Similarly:
which again results in $JE_j^2 + OE_o^2 = CB^2 = 2EM^2$. Analogously, we find $KE_k^2 + LE_l^2 = CB^2 = 2EM^2$, and so on. Denoting the points on the parabola as $E_0 = A, E_1, E_2, \cdots, E_n = B$ (with $n=2^m$) corresponding to points on the axis $F_0 = A, \cdots, F_{n/2} = M, \cdots, F_n = C$, we obtain:
and hence:
Let $S_i = \pi (\overline{E_iF_i})^2$ be the areas of the disks of radius $E_iF_i$ for $(1 \le i \le n-1)$, and let $S_n$ be the area of the disk of radius $E_nF_n = BC$. Then:
Let $W_i$ be the volume of the cylinders with base $S_i$ and height $h = \frac{\ 1\ }{n}AC$, and $W_n$ the volume of the cylinder with base $S_n$ and height $h$. Then:
Now,
since $V = nW_n$, so $\sum_{i=1}^{n-1} W_i < \frac{\ 1\ }{2}V$. But we also have $\sum_{i=1}^{n-1} W_i = v-v_n > \frac{\ 1\ }{2}V$, which is impossible. Therefore, $v \le \frac{\ 1\ }{2}V$.
Next, suppose that $v < \frac{\ 1\ }{2}V$, that is $v + \epsilon = \frac{\ 1\ }{2}V$, and proceed as before. We again remove half of the volume of the cylinder, then half of the remainder, until the remaining volume $V_n$ is less than an arbitrarily small $\epsilon$. Let $u_n$ be the portion of $V_n$ external to the paraboloid. Then $u_n < V_n < \epsilon$, and so $v + u_n < \frac{\ 1\ }{2}V$. But:
Also, $\sum_{i=1}^{n-1} W_i = \sum_{i=1}^{n} W_i - W_n$, so:
Hence, $\sum_{i=1}^n W_i > \frac{\ 1\ }{2}V$, which is again impossible. Therefore, $v \ge \frac{\ 1\ }{2}V$.
Thus, we have shown that $v = \frac{\ 1\ }{2}V$ in the case where $\angle ACB$ is a right angle. Ibn al-Haytham addresses the other two cases, where $\angle ACB < \pi/2$ and $\angle ACB > \pi/2$, by applying an affine transformation: oblique axes are converted into rectangular axes. More precisely, he maps each point of the figure in either of the two cases to the corresponding point in the first case, using the preservation of relationships within the figures. This is therefore a method that combines integral summation and the method of exhaustion, supported by a solid arithmetic foundation.
Ibn al-Haytham’s method becomes particularly evident in his treatment of the second kind of paraboloid – namely, that obtained by rotating a parabola around an ordinate. To better highlight the nature of his approach, let us describe his study using a different notation. Consider the paraboloid generated by rotating the sector $ABC$ of the parabola $x = ky^2$ about the ordinate $BC$. Let $AC=c$ and $BC=b$. Let $\sigma_n = (y_i)_{0 \le i \le 2m}$ with $2m=n$, a subdivision of the interval $[0, b]$ with step $h=b/n$. Let $M_i$ be the points on the parabola with ordinate $y_i$ and abscissa $x_i$, and define $r_i = c - x_i$ for $0 \le i \le 2^m = n$. It follows that $r_i = k(b^2 - y_i^2) = kh^2(n^2 - i^2)$. Denoting by $I_n$ and $C_n$ the volumes of the inscribed and circumscribed cylinders, we have:
and by inequality (59):
where $V = \pi k^2 b^4 \cdot b$ is the volume of the circumscribed cylinder. Still using a modern formalism not present in Ibn al-Haytham’s original, we can express the calculation as follows. Since the function $g(y) = ky^2$ is continuous on $[0, b]$, denoting the volume of the paraboloid by $v(p)$, we have:
that is:
thus:
yielding:
where $V$ is again the volume of the circumscribed cylinder.
Finally, Ibn al-Haytham investigates the behavior of solids approximating the paraboloid from the outside as the number of subdivision points increases. He essentially addresses the problem of the variation in the ratio between the inner and outer infinitesimal solids approximating the paraboloid. While in the case of the first kind of paraboloid both solids have the same volume, this is not the case for those of the second kind. Denoting the volumes of the inner and outer approximating solids by $v_n$ and $u_n$ respectively, he proves that:
Let $u(m)$ and $W(m)$ be the corresponding values at the $m$-th subdivision (with $n = 2^m$). He demonstrates that:
hence the ratio increases with finer subdivisions. This reflects a clearly infinitesimal orientation and, to some extent, a theory of functions. The goal is explicit: to understand the asymptotic behavior of mathematical objects by studying their variation.
Following the treatise on paraboloids, Ibn al-Haytham addresses the volume of the sphere in another treatise titled Qawl fī misāḥat al-kura (On the Measurement of the Sphere), in which he applies the same method. He begins similarly, by introducing the necessary arithmetic lemmas. He first recalls:
and establishes the inequality:
Using the same method as before, he proves that the volume of the sphere equals two-thirds that of the circumscribed cylinder. Let us now examine the integral approach underpinning this method. To determine the volume of revolution about a given axis, he considers inscribed and circumscribed cylindrical slices whose axis coincides with that of the solid of revolution. This yields lower and upper approximations of the volume using integral sums (Darboux sums) corresponding to the function that generates the solid.
For example, in the case of the sphere:
where the function $f$ is monotonic and:
for $x_{i-1} \le x \le x_i$, with $m_i$ and $M_i$ being values at the endpoints of the $i$-th subinterval. He then uses the inequalities $I_n < v < C_n$, and shows that for any $\epsilon > 0$, there exists an $N$ such that for all $n \ge N$, we have $v - I_n < \epsilon$ and $C_n - v < \epsilon$, demonstrating that $I_n \to v$ and $C_n \to v$. In other words, the volume $v$ equals the integral $\int_0^R f(x)\, dx$. Ibn al-Haytham’s calculation thus effectively corresponds to a simple Cauchy-Riemann integral.
This mathematical equivalence, however, should not obscure the following question: why did Ibn al-Haytham, after determining volumes by means of this integral, never provide a general method for determining other volumes and areas? To answer this question satisfactorily, it is not enough to invoke the specific needs of Ibn al-Haytham. In his mathematical, optical, and astronomical works, he never required the calculation of the volume of a paraboloid – nor, for instance, of a hyperboloid of revolution. The absence of such a general method must therefore be attributed to the method itself.
Indeed, one may observe that, like his predecessors in dealing with areas, Ibn al-Haytham always appeals to another solid with a known volume against which to compare the given solid. This prior knowledge of the comparison solid is not an artifice of the method: it allows Ibn al-Haytham, as it did his predecessors, to perform an effective, direct, and exact calculation of the limits of the corresponding Darboux sums. Yet in the general case, such comparison solids may not exist. This renders the mathematical tools employed by Ibn al-Haytham inadequate for effectively computing Darboux sums. It is therefore a genuine internal limitation that characterizes his method.
Nonetheless, one must be careful not to overstate the significance of this limitation – a limitation that would later disappear with the more extensive development of arithmetic calculus. If the use of a reference volume well characterizes the Archimedean tradition, the growing arithmetic orientation in the Arab mathematical tradition shows that it was no longer strictly a matter of Archimedean inheritance. Ibn al-Haytham was guided not only by geometry but already by arithmetic; his lemmas arise from an arithmetical conception of geometric figures.
In this study, one can already observe the development of the tools and techniques of this branch of mathematics in the Arabic world. We have seen how Ibn al-Haytham, in his investigations on the paraboloid, attained results later attributed by historians to figures such as Kepler and Cavalieri. These inquiries, however, came to a halt – most likely due to the absence of an effective symbolic notation.
Among the problems concerning the determination of the areas of curved surfaces, the exact quadrature of the 'lunules' – surfaces bounded by two arcs of a circle – is one of the oldest. According to later sources such as Simplicius, the 6th-century commentator of Aristotle, the problem dates back to Hippocrates of Chios in the 5th century BCE. In his commentary on Aristotle’s Physics, Simplicius quotes a long passage from Eudemus, a disciple of Aristotle, which contains the results and methods of Hippocrates. This passage, which also raises several philological and historical questions, is the only known source for the history of this problem in Greek mathematics. It also indicates the context in which the problem of the quadrature of certain lunules was posed, in this case as part of the problem of squaring the circle.
About five centuries after Simplicius, Ibn al-Haytham repeatedly returned to this question, initially in connection with the quadrature of the circle, and later as a problem in its own right. In fact, he revisits it in three treatises, only one of which – the one on squaring the circle – has been studied until now, while another short one is dedicated to the quadrature of the lunules. Later, he returned to the subject, obtaining results that would be attributed to mathematicians of the 17th and 18th centuries. The lack of awareness of Ibn al-Haytham’s work, particularly of this latter treatise, has led historians to make, in complete good faith, erroneous assessments of his contributions to these investigations.
Everything suggests that Ibn al-Haytham’s starting point was the text attributed to Hippocrates of Chios. In his first treatise, Qawl fī ’l-hilāliyyāt (Treatise on the Lunules), he begins by saying: “when I considered [...], the figure of the lunules equal to a triangle, mentioned by the ancients [...]”. Later, in a second treatise, Maqāla mustaqṣā fī ’l-ashkāl al-hilāliyya (Exhaustive Treatise on the Figures of the Lunules), Ibn al-Haytham recalls his earlier book by stating: “I composed a short treatise on the lunules according to particular methods” (Rashed 1993a, p. 102). The results of Hippocrates of Chios are also mentioned in his works. Did Ibn al-Haytham become familiar with them through Simplicius’s commentary on Aristotle’s Physics, which might have been translated into Arabic at the time? We have no documents that allow us to answer this question precisely. In his first work, Ibn al-Haytham refers to the ‘ancients’, but does not reproduce any of Hippocrates’s figures. Nevertheless, his first result slightly generalizes a proposition by Hippocrates, cited by Simplicius based on a text by Alexander of Aphrodisias; this significantly complicates the problem. It is proposition 3, which also appears in his work on squaring the circle (Qawl fī tarbīʿ al-dāʾira), and in his second treatise (prop. 8). In any case, let us now turn to Ibn al-Haytham’s two works.
The method adopted in both consists of studying lunules bounded by arbitrary arcs and seeking equivalences between surfaces. The author introduces circles equivalent to sectors of circles given in the problem and expressed as fractions of the latter. He justifies the existence of the introduced circles, which he adds to or subtracts from polygonal surfaces to obtain a surface equivalent to that of a lunule, or the sum of two lunules.
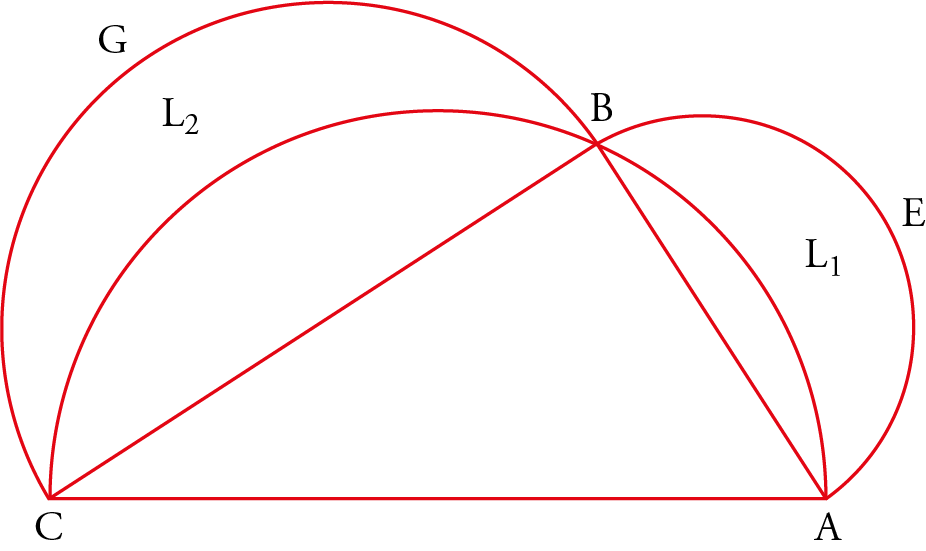
In the first short treatise, in propositions 1, 2, and 5, he begins with a semicircle $ABC$ to study lunules $L_1$ and $L_2$ bounded by an arc $AB$ or $BC$ and a semicircle (fig. 18). He assumes that the arc $AB$ is equal to one-sixth of a circle and establishes the following results:
where $L_3$ is a lunule similar to $L_1$ such that $L_3 = L_1$, and $\mathscr {C}(ABC)$ and $\text{tr}(ABC)$ denote respectively the circle $ABC$ and the triangle $ABC$.
In proposition 3, he slightly generalizes the demonstration of the result of Hippocrates of Chios by considering an arbitrary point B on the semicircle $ABC: L_1 + L_2 = \text{tr}(ABC)$; and in proposition 4, he studies the ratio between two similar lunules. It should be noted that in these propositions the lunules L₁ and L₂ involved are those associated with the three semicircles $ABC$, $AEB$, and $BGC$.
This first treatise thus follows in the footsteps of the research of Hippocrates of Chios. The same applies to the part concerning the lunules in the work Fī tarbīʿ al-dāʾira. Like Hippocrates, Ibn al-Haytham uses the proportionality between the area of a circle and the square of its diameter, and the Pythagorean theorem. In both cases, the lunule associated with the isosceles right triangle is studied. Even though Ibn al-Haytham’s reasoning is somewhat more general, this generalization does not fundamentally alter the similarity between his procedure and that of Hippocrates. For the sake of completeness, it should be noted that what is important in Fī tarbīʿ al-dāʾira is not the results on lunules, which he studies as in the first treatise, but the distinction he establishes between the existence of a square equivalent to a circle – that is, in modern terms, the existence of a transcendental ratio – and the constructibility of this square or ratio.
The situation is very different in the second treatise, Maqāla mustaqṣā fī ’l-ashkāl al-hilāliyya. Not only does he obtain more general results here, but the procedure is not the same. He returns to the problem of the quadrature of the lunules, moves it to the plane of trigonometry, and seeks to deduce the different cases as various properties of a trigonometric function that would be recognized much later by Euler. From the outset, he explicitly acknowledges that the calculation of the areas of lunules involves sums and differences of areas of circular sectors and of triangles, the comparison of which requires the comparison of ratios between angles and ratios between segments. For this reason, he begins by establishing four lemmas concerning triangle $ABC$, right-angled at $B$ in the first lemma and with an obtuse angle in the other three (figs. 19, 20), which now show that the essential point of the research has become the study of the function
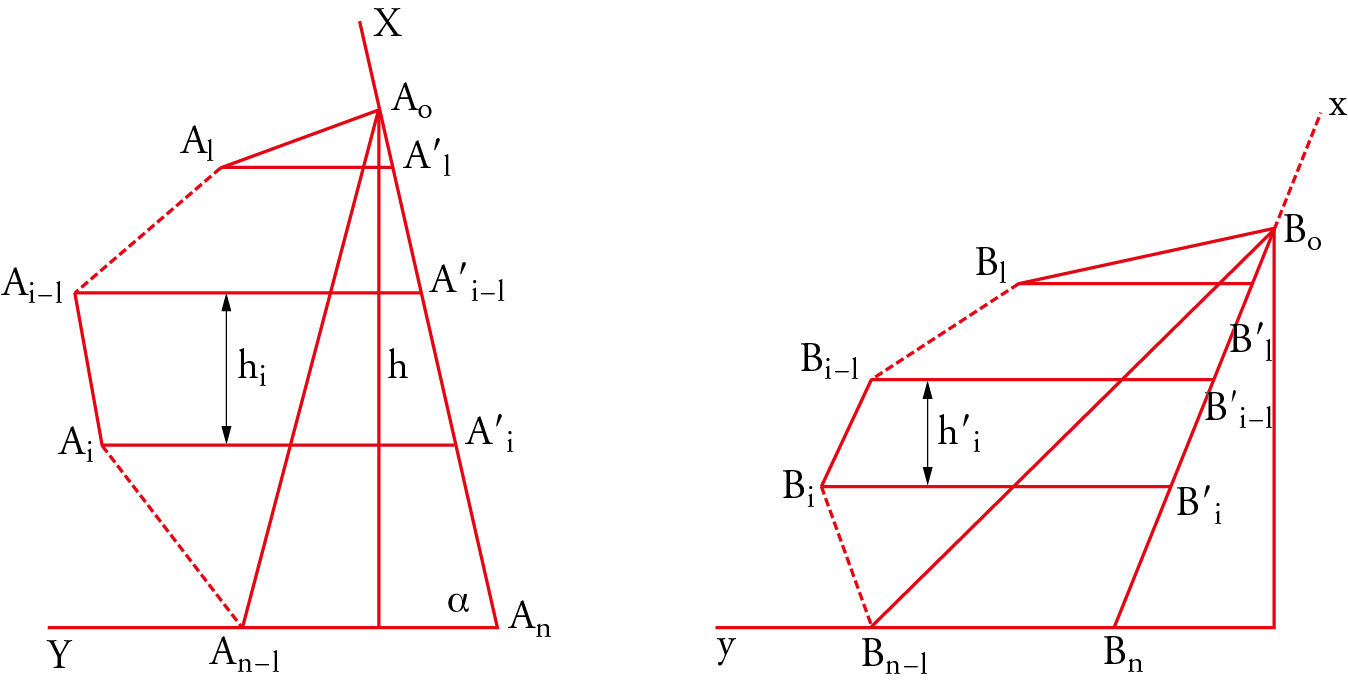
The first lemma states the following. Given two convex polygons $A = (A_0, A_1,\cdots, A_n)$ and $B = (B_0, B_1,\cdots, B_n)$, let the points $A_1,\cdots, A_{n-1}$ be projected onto $A_0A_n$ parallel to $A_{n-1}A_n$ at points $Ac_1,\cdots, A^{\prime}_{n-1} = A_n$, and the points $B_1,\cdots, B_{n-1}$ onto $B_0B_n$ parallel to $B_{n-1}B_n$ at points $B^{\prime}_1,…, B^{\prime}_{n-1} = B_n$. If:


a) If $0 < C < \pi /4$ and $A < \pi /2$, then $(\sin^2 C)/C < 2/ \pi < (\sin^2 A)/A$; it is clear that if $C = A = \pi /4$, then $(\sin^2 C)/C = (\sin^2 A)/A = 2/ \pi$.
b) Let $\pi – B=B_1$; if $C < \pi /4$ and $B_1 < \pi /2$, then $(\sin^2 C)/C < (\sin^2 B_1)/B_1$.
c) If $A \le \pi /4$, then $(\sin^2 A)/A < (\sin^2 B_1)/B_1$.
d) Here he proposes to study the case $A > \pi /4$. The study, however, is incomplete: Ibn al-Haytham demonstrates that, given $A$, one can find $B_0$ such that
This incomplete study seems to have prevented him from seeing the equality
\begin{equation} \frac{\sin^2{A}}{A}=\frac{\sin^2{B_1}}{B_1} \ \text{.} \end{equation}It will be noted that these lemmas, by linking the problem of the quadrature of the lunules to trigonometry, change its status and allow the various particular cases to be unified. But the previously mentioned incompleteness conceals the possibility of the existence of squarable lunules. Let us now briefly turn to the propositions of Ibn al-Haytham’s second treatise.
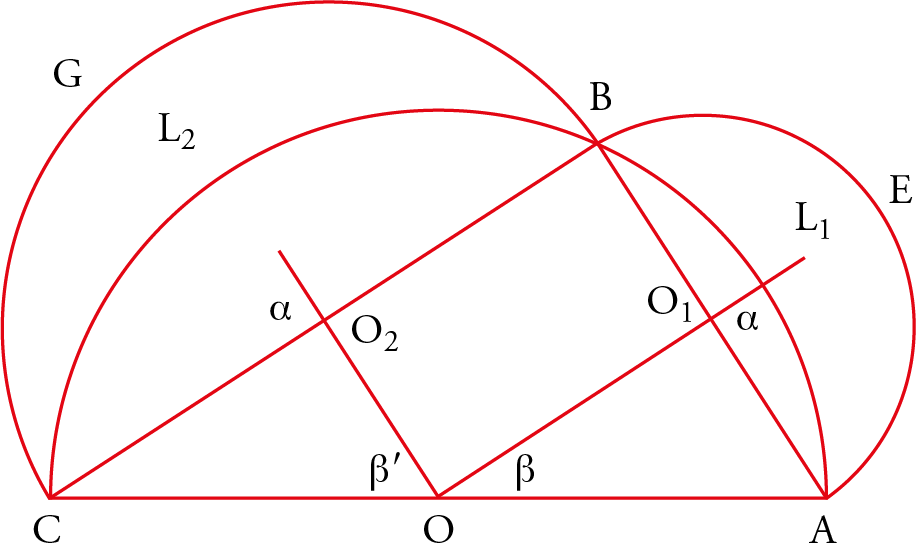
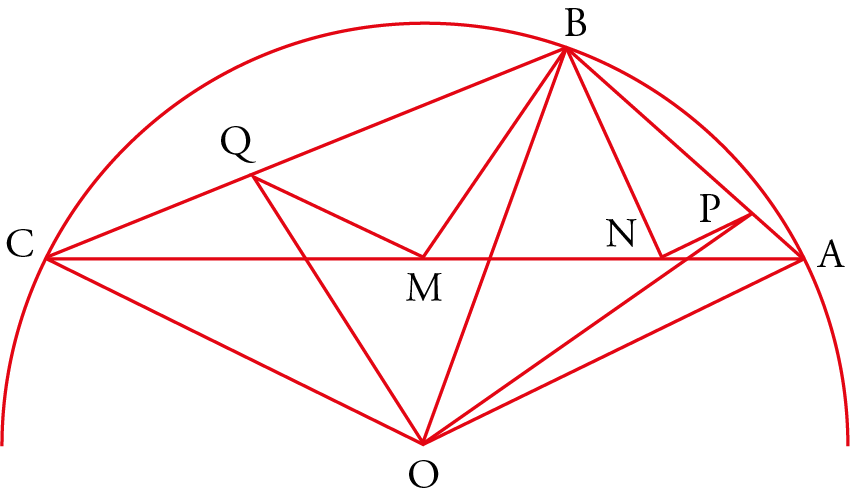
In nine propositions, from 8 to 16, the lemmas are paired, and in all cases, the three arcs $ABC$, $AEB$, and $BCG$ are similar. Let $O$, $O_1$, and $O_2$ be the centers of the corresponding circles (fig. 21).
Let us set $\angle AOC = \angle AO_1B = \angle BO_2C = 2\alpha, \angle AOB = 2\beta$, and $\angle BOC = 2\beta^{\prime}$, with $\beta \le \beta^{\prime}$ and $\beta - \beta^{\prime} =\alpha$.
The lunule $L_1$ is characterized by $(\alpha, \beta) $ and the lunule $L_2$ by $(\alpha, \beta^{\prime})$. The case $\alpha =\pi /2$ is considered, and the following propositions are established:
1. For every pair $(\beta, \beta^{\prime})$ such that $\beta + \beta^{\prime}= \pi /2$, we have $L_1 + L_2 = \text{tr}(ABC)$;
2. For $\beta = \beta^{\prime}= \pi /4$, we have $L_1 = L_2 = \text{tr}(ABC)/2$; in this case, $\alpha / \beta = 2/1$, and this is the only squarable lunule studied by Ibn al-Haytham. For $\beta < \beta^{\prime}$ we have:
where the circle $N$ depends on the ratio $\alpha / \beta$.
3) For $\beta = \pi /6$, we have $L_1 = (1/2)·\text{tr}(ABC) - (1/24) \mathscr {C} (ABC)$; in this case, $\alpha / \beta = 3/1$. For $\beta^{\prime} = \pi /3$, we have $L_2 = (1/2)·\text{tr} (ABC) + (1/24)·\mathscr {C} (ABC)$, and in this case $\alpha / \beta = 3/2$.
Up to this point, only Lemma 1 is used in the proofs. To establish the next proposition, the other three are employed. The guiding idea is to start from points $M$ and $N$ on chord $AC$ such that $\angle ABC = \angle BMC = \angle ANB = \pi - \alpha$, and to define a point $P$ on $AB$ and a point $Q$ on $BC$ such that $NP$ is parallel to $OA$ and $MQ$ is parallel to $OC$ (fig. 22); the results can no longer be established from triangle $ABC$ as in the previous propositions.
For every pair $(\beta, \beta^{\prime})$ such that $\beta + beta^{\prime} < \pi /2$, he then defines two circles $(K)$ and $(Z)$ such that:
\begin{align} L_1+L_2+(K)&=\text{quadrilateral}(OPBQ) \notag \\ L_1+(Z)&=\text{tr}(OPB) \end{align}
He then considers the following cases:
If $\beta = \beta^{\prime}$, then $(Z) = (K)/2$, $L_1 = L_2$, and $L_2 - (Z) = \text{tr}(OQB) = \text{tr} (OPB)$;
If $\beta^{\prime} < \pi /4$, then $(Z) < (K)$ and $L_2 − ((K) - (Z)) = \text{tr} (OQB)$;
If $\beta^{\prime} > \pi /4$, then either $(Z) < (K)$, $L_2 = \text{tr} (OQB) + ((Z) - (K))$ and $L_2 > \text{tr} (OQB)$, or $(Z) = (K)$ and $L_2 = \text{tr} (OQB)$, or again $(Z) > (K)$, $L_2 = \text{tr} (OQB) + ((Z) - (K))$ and $L_2 > \text{tr} (OQB)$. He illustrates these results with examples, then proves the following propositions.
4) If $\alpha = \pi /3$, $\beta = \beta^{\prime}= \pi /6$, $\alpha / \beta = 2/1$, then:
\begin{equation} fL_1+L_2=\frac{2}{3}\text{tr}(ABC)-\frac{\ 1\ }{18}\mathscr {C} (ABC) \ \text{.} \end{equation}5) If $\alpha = \pi /3$, $\beta = \pi /12$, $\beta^{\prime} = \pi /4$, $\alpha / \beta = 4/1$, $\alpha / \beta^{\prime} = 4/3$, in this case the relevant circle is not part of the circle $ABC$.
6) If $\alpha = \pi /3 + \pi /8$, $\beta = \pi /8$, $\beta^{\prime} = \pi /3$, $\alpha / \beta = 11/3$, $\alpha / \beta^{\prime} = 11/8$, in this case the circle involved is not part of the circle $ABC$.
In the following propositions, with the exception of prop. 21, he studies figures composed of sums or differences of lunules, segments, and triangles. In proposition 21, he indicates a property of the lunule whose two arcs belong to two equal circles, a property resulting from the translation that relates the two circles and which he studies in the treatise Fī ’l-taʿlīl wa-’l-tarkīb (On Analysis and Synthesis).
With this second treatise, Ibn al-Haytham's study of the quadrature of lunules takes a new direction, one that would later lead to Euler, shifting the problem towards trigonometry and revealing its dependence on function [86].
We have emphasized how infinitesimal geometry emerged in fields beyond the determination of areas and volumes of curved figures. One such field is the study of isoperimetric problems in the plane and in space. Initially linked to astronomy, this line of inquiry gradually distanced itself from it to become a chapter of infinitesimal geometry. This is not the place to retrace in detail the history of this process; it will suffice to outline its general contours.
Among plane figures with a given perimeter, the circle has the maximum area, and among solids with the same total surface area, the sphere has the maximum volume. This is the statement of the extremal problem, which has continuously attracted the interest of mathematicians and astronomers since Antiquity: while the latter needed it to establish the sphericity of the heavens and the world-body, the former likely undertook the task of providing the missing proof.
According to the testimony of Simplicius, a 5th-century philosopher, the isoperimetric problem is ancient. He writes: “It has been demonstrated, not only before Aristotle – so much so that he used it as a proven proposition – but also by Archimedes, and more extensively (platēteron) by Zenodorus, that among isoperimetric figures, the most extensive is, among plane figures, the circle, and among solids, the sphere” (Simplicii in Aristotelis de Coelo Commentaria, VII, 4/2, ll. 12-17).
This important, albeit late, text shows – as noted by W. Schmidt (1901) – that the fundamental propositions were known before Zenodorus. This idea later led J. Mogenet (1961) to attribute to Zenodorus only the merit of a first formulation of a full-fledged isoperimetric theory and to date the mathematician to the 3rd century BCE. The issue remains controversial, then as now; all that can be said at present is that Zenodorus lived after Archimedes and before Pappus, that is, between the 2nd century BCE and the 3rd century CE.
An interval of half a millennium naturally invites debate, especially in the absence of further clarifying details still awaited. Yet these debates, already underway at the beginning of the last century, have not prevented historians from agreeing in attributing to Zenodorus the treatment of the mathematical problem and its demonstration. Fortunately, Theon of Alexandria (4th century CE) summarizes Zenodorus’s book in his Commentary on the First Book of the Almagest. After stating the isoperimetric problem, Theon explicitly announces that “he will demonstrate it in an abbreviated way, drawn from the demonstration by Zenodorus, in the treatise on isoperimetric figures” (p. 33). Theon directly draws from Zenodorus to comment on the famous Ptolemaic formula in Book I of the Almagest: “Since among the various figures with equal perimeter, those with more sides are larger, the largest among plane figures is the circle, and among solid ones the sphere, and the sky is the largest of all bodies” (ed. Heiberg, p. 13, ll. 16-19).
From Theon’s time onward, commentaries on the Almagest could no longer ignore such a formulation, which touches on a fundamental idea in astronomy, cosmology, and philosophy: the sphericity of the heavens and the world-body. They had to provide a demonstration. Naturally, other mathematicians also took interest in this problem, such as Heron of Alexandria and Pappus of Alexandria (4th century BCE), in Book V of the Collection. Theon’s Commentary, as well as the Almagest itself – both known to 9th-century astronomers and mathematicians – stimulated a new tradition of research into isoperimetric problems beginning with al-Kindī, who claims to have considered the problem “in [his] book on spheres.” In Fī ’l-ṣināʿāt al-ʿuẓmā (On the Great Art), he writes: “Similarly, since the largest of the figures in the circle having equal sides is the one with the most angles, and the largest solid figure with equal and flat surfaces is the sphere, as we explained in our book On Spheres, the sky is therefore greater than all other bodies, and is spherical because it must have the greatest shape” (Istanbul, Aya Sofya, 4860, f. 59v).
The 13th-century biographer and bibliographer Ibn Abī Uṣaybiʿa lists among al-Kindī’s works one explicitly dedicated to this problem: Fī anna al-kura awsāʿ al-ashkāl al-mujassama (The Sphere is the Largest Solid Figure). In any case, al-Kindī’s Ṣināʿāt al-ʿuẓmā strongly reflects the influence of Theon.
This tradition includes, to various extents, many astronomers like Jābir ibn Aflah and mathematicians such as Ibn Hūd. But two scholars transformed the research in this field, each in his own way: al-Rāzī and Ibn al-Haytham. They are the principal figures currently known. The reading and analysis of their writings will highlight the great distance between them: while al-Rāzī develops the past, Ibn al-Haytham, by completing it, touches upon the future.
Abū Jaʿfar al-Ḥāzin (10th century) also wrote a Sharḥ al-maqāla al-ʾūlā min al-Majisṭī (Commentary on Book I of the Almagest). It is likely in connection with the famous statement by Ptolemy previously cited that he includes in this work a treatise with the aim of providing a rigorous demonstration. al-Ḥāzin is clear in this regard: he wants to establish Ptolemy’s statement not through calculation (ḥisāb) but by geometric means. An examination of the text clearly shows that although al-Ḥāzin knew of Zenodorus’ results from Theon’s summary, he nevertheless follows a different path, as we will see. The guiding idea of al-Ḥāzin, of which he is fully aware, is the following: among all convex figures of a given type (triangle, rhombus, parallelogram, etc.), the most symmetrical realizes an ‘extreme’ for a certain quantity (area, area ratio, perimeter, etc.). The process is as follows: a parameter is fixed, and the figure is varied by symmetrizing it with respect to a given line. For example, fixing the perimeter of a parallelogram, it is transformed into a rhombus by making it symmetrical with respect to a diagonal: in the transformation process, the area increases. Not only does this idea distinguish al-Ḥāzin’s contribution from those of his predecessors, but forgetting it would mean missing the meaning of this contribution.
al-Ḥāzin’s treatise has a simple structure. In the first part, the author deals with isoperimetric problems in the plane and in the second, in space. Both parts depend on unspecified notions and unarticulated axioms. In particular, the notion of convexity: all polygons and polyhedra considered are convex. Among the other axioms are the following:
(A1) if a convex polygon is inscribed in a circle, then its perimeter is less than that of the circle;
(A2) if a convex polygon is circumscribed around a circle, then its perimeter is greater than that of the circle;
(A3) if a convex polyhedron is inscribed in a sphere, then its surface area is less than that of the sphere;
(A4) if a convex polyhedron is circumscribed around a sphere, then its surface area is greater than that of the sphere.
These axioms are necessary to rigorously demonstrate an important lemma (the eighth) and a proposition (number 19). Let us briefly consider the two parts of the treatise.
In the first part, before establishing the isoperimetric theorem, al-Ḥāzin proves eight lemmas. The first four concern isosceles and equilateral triangles, and show that the area of an equilateral triangle is greater than that of any isosceles triangle with the same perimeter. The fifth shows that the area of an equilateral triangle is greater than that of any triangle with the same perimeter. In the course of the demonstration, he establishes a result already expressed by Zenodorus and Pappus, namely that among isoperimetric figures with the same number of sides, the largest is that which has equal sides and angles. In Lemma 6, he compares a parallelogram to a square with the same perimeter. In Lemma 7, he considers the example of a regular pentagon, deduces an irregular one with the same perimeter, and shows that the latter has a smaller area.
Let us pause for a moment and compare this method with that of Zenodorus. The latter begins by comparing an arbitrary triangle and an isosceles triangle with a common base and the same perimeter, to arrive at the following lemma: the sum of two similar isosceles triangles with different bases is greater than the sum of two non-similar isosceles triangles with the same perimeters as the two similar triangles. Here, “same perimeter” means that the sums of the sides, excluding the bases, are equal. This lemma by Zenodorus is, however, incorrect, and it is surprising that neither Pappus nor Theon noticed the error. This lemma is essentially equivalent to maximizing $ax+by$ under the constraint $\sqrt{1 + 2a^2x^2} + \sqrt{1 + 2b^2y^2} = 1$. It is thus necessary that $ax>by$, hence $x>b$ and $y<2a$, and differentiating the second equality,
\begin{equation} \frac{bx}{\sqrt{a^2+x^2}}=\frac{ay}{\sqrt{b^2+y^2}}\ ;. \end{equation}Setting $x=au$, $y=bv$, we obtain:
\begin{equation} \frac{u}{a\sqrt{1+u^2}}=\frac{v}{b\sqrt{1+v^2}}\ ; \end{equation}While the stated proposition requires $u=v$. Could this error be what led al-Ḥāzin to choose a different method?
In Lemma 8, finally, he moves on to convex polygons, assuming the existence of both an inscribed and a circumscribed circle.
Everything is now in place to establish the isoperimetric property of regular polygons before finally stating the theorem concerning the circle. He first proves that if two regular polygons $P_1$ and $P_2$ have respectively $n_1$ and $n_2$ sides, with $n_1 > n_2$, and the same perimeter, then the area of $P_1$ is greater than that of $P_2$. He then establishes the theorem: among all plane figures – regular convex polygons and circles – having the same perimeter, the circle encloses the largest area.
As for isoperimetric problems in the plane, al-Ḥāzin proceeds (a) by comparing regular polygons with the same perimeter and different numbers of sides; (b) by comparing a regular polygon and a circle with the same perimeter using a similar polygon circumscribed around the circle. This approach is common to al-Ḥāzin and Zenodorus. It is a static approach, in the sense that on one side we have the given polygon and on the other the circle. Later, Ibn al-Haytham would use (a) to establish (b), by considering the circle as the limit of a sequence of regular polygons. This represents a dynamic approach. In other words, even though al-Ḥāzin's method is different from that of Zenodorus or Pappus, it is of the same type, while Ibn al-Haytham’s is of a different type.
The second part of al-Ḥāzin’s treatise addresses the same extremum problem, but in space. This section also consists of nine lemmas concerning the surface area and volume of the pyramid, cone, and truncated cone. In the first lemma, he considers the lateral area of a regular pyramid; in the second, the volume of a pyramid admitting an inscribed sphere; in the third, the lateral area and volume of a cone of revolution; the fourth lemma considers the following problem: given a circle $C$, construct two similar polygons with areas $S_1$ and $S_2$, one circumscribed about $C$ and the other inscribed in $C$, such that $S_1/S_2 = k$ (a given ratio). In the fifth lemma, he provides another expression for the lateral area of the cone, and in the sixth, he considers the area of a truncated cone. From the latter, he deduces the seventh lemma: if a regular polygonal line is inscribed in a circle of area $S_1$ and circumscribed about one of area $S_2$, the area $S$ of the surface generated by rotating this line around one of its axes satisfies $ 4S_2 < S < 4S_1$.
Let us recall that in propositions 27 through 30 of On the Sphere and Cylinder, Archimedes obtained the same results for a solid defined by a regular polygon with a number of sides that is a multiple of 4. The Banū Mūsā later addressed the same problem for a solid defined by a polygonal line inscribed in a semicircle and with an even number of sides (propositions 12 and 13). This is precisely the case treated by al-Ḥāzin. John of Tynemouth, in proposition 5, also studied the same result based on a regular polygon inscribed in a circle and having a number of sides that is a multiple of 4 or simply of 2.
Al-Ḥāzin concludes by establishing two fundamental propositions. In the first, he shows that the surface area S of the sphere is equal to four times the area of a great circle. Archimedes had presented the same theorem in proposition 33 of Book I of On the Sphere and Cylinder, and the Banū Mūsā in proposition 14 of the treatise Kitāb maʿrifat misāḥat al-ashkāl al-basīṭa wa-’l-kuriyya (Book for Knowing the Area of Plane and Spherical Figures). In the second proposition, al-Ḥāzin reconsiders the determination of the volume of the sphere, $V = (1/3)RS$, where $R$ is the radius of a great circle and $S$ the surface area. To establish this proposition, he uses a proof by contradiction and applies proposition 17 of Book XII of the Elements, following a method similar to that used by the Banū Mūsā.
Finally, he proves the theorem asserting that among all convex solids with the same surface area, the sphere has the maximum volume. Given a sphere with center $O$, radius $R$, surface area $S$, and volume $V$, and a polyhedron with the same surface area $S$ and volume $V_1$, which is assumed to be circumscribed about another sphere of radius $R^{\prime}$ and surface area $S^{\prime}$, then $V_1 = (1/3)SR^{\prime}$. Since $S^{\prime}$ is less than the surface area of the polyhedron, we have $S > S^{\prime}$, hence $ R^{\prime} < R$ and $(1/3)S R^{\prime} < (1/3)SR$, i.e., $V_1 < V$. Note that the specific type of polyhedron is not identified, but the proof assumes it is circumscribed about a sphere, i.e., a regular polyhedron. This proof does not apply to arbitrary polyhedra or solids.
As we can see, al-Ḥāzin’s approach is not the same in space as in the plane. This time he does not compare polyhedra with the same surface area and a different number of faces, but instead reaches the result using the formula linking the volume of the sphere to its surface area – a formula he derives by approximating the sphere with irregular polyhedra. Ibn al-Haytham’s method, as we shall see, will again be entirely different.
About half a century after al-Hāzin, Ibn al-Haytham revisited the same problem, but restoring to it, so to speak, its horizon, that of the study of asymptotic behaviors. It was thus no longer a matter of writing an introduction to the Almagest to justify Ptolemy’s famous statement in the first book of that work, but of composing a treatise entirely dedicated to the study of the problem itself and explicitly tackling its asymptotic nature. Ibn al-Haytham indeed set out to establish that “among figures with similar [and equal] perimeters, the circle has the largest [area], and that among polygons, the one that most closely approximates the circular form is larger than one that departs from it” (Rashed 1993a, p. 394), and more generally that among “solid and planar” figures, the one approaching the circular form “has a greater measure than that which departs from it” (ibid., p. 384). Let us briefly examine the approach he took.
He resolves the isoperimetric problem in the plane in three propositions and one lemma. Here are the three propositions in order. Proposition 1 asserts that, if $p$ is the perimeter of a circle and $A$ the area, $p^{\prime}$ the perimeter of a regular polygon and $A^{\prime}$ the area, if $p = p^{\prime}$, then $A > A^{\prime}$. Proposition 2 states: given $P_1$ and $P_2$, two regular polygons with $n_i$, $p_i$, and $A_i$ $(i = 1,2)$, the number of sides, perimeters, and areas, if $p_1 = p_2$ and $n_1>n_2$, then $A_1>A_2$. Finally, Proposition 3 establishes that, given $P_1$ and $P_2$, two regular polygons inscribed in the same circle (with the same notation), if $n_1>n_2$, then $p_1 > p_2$ and $A_1>A_2$. To prove this last proposition, he demonstrates a lemma which can be stated as: $\alpha/ \beta = \sin \alpha / \sin \beta$, for $\pi /2 > \alpha > \beta$.
To establish the isoperimetric property, he thus shows that the area of a circle is like a ‘limit’ of an increasing sequence of areas of regular polygons. In the proof, he assumes that this limit exists, as already acknowledged in Archimedes’ Measurement of the Circle. He thus embarks on an expressly “dynamic” procedure, apparently different from that of his predecessors. This may explain what he writes at the beginning of the treatise: “Mathematicians have evoked this notion [of isoperimetry] and used it. However, none of their proofs have come down to us” (ibid., p. 386). Now, it is unlikely that Ibn al-Haytham was unaware of his predecessors’ numerous results, including those of al-Hāzin. Rather, everything seems to indicate that he wanted to draw the reader’s attention to the novelty of his procedure.
After tackling the isoperimetric problem in the plane, he moves on to that in space (concerning solids with equivalent surfaces), which he addresses using a similar method. However, the transition from plane to space is not always easy. On his path, he thus encounters an obstacle that will prevent him from achieving his goal, though not from composing a mathematical text that, until the mid-17th century, would remain among the most advanced. Analogous to the first part of the treatise, he sets out to prove the following two propositions: among two regular polyhedra with similar faces and the same total surface area, the one with the greater number of faces has the greater volume; among two regular polyhedra with similar faces inscribed in the same sphere, the one with the greater number of faces has both greater surface area and volume. He thought he could establish the isoperimetric property as the limit of a sequence of areas of polyhedra, i.e., approximate the sphere with the infinite sequence of polyhedra circumscribed about it. The obstacle lies in the fact that these previous propositions concern regular polyhedra, and their number is finite.
Much of the treatise consists in proving these two propositions. For this purpose, he begins by establishing five lemmas (lemmas 6 through 10), all of which deal with inequalities involving ratios of solid angles and areas. This is, to our knowledge, the first major and extensive application of the solid angle and therefore also the first considerable study of some of its properties. By means of these lemmas, he establishes, in full generality, the aforementioned propositions. These, however, only apply to the tetrahedron, octahedron, and icosahedron, since the number of faces of a regular polyhedron with square or pentagonal faces is fixed (6 or 12). The first proposition thus means that if a tetrahedron, an octahedron, and an icosahedron all have the same surface area, then their volumes increase in that order. The second states that if a tetrahedron, octahedron, and icosahedron are inscribed in the same sphere, their volumes likewise increase in that order. Thus, one cannot approximate the sphere with an infinite sequence of regular polyhedra. Such an oversight by a mathematician who knew Euclid’s Elements better than anyone is surprising. How could he not see that these polyhedra are only those mentioned by Euclid? That their number is finite? This oversight should not, however, overshadow the richness of the treatise. Let us pause here at the proof of the two propositions.
The idea of the proof of the first proposition can be summarized as follows. Let $A$ (respectively $B$) be the center of the sphere circumscribed about the first (second) polyhedron, $AE$ ($BG$) the distance from the center to the plane of one of the faces, $SA$ ($SB$) the total surface area of the polyhedron, and $VA$ ($VB$) the volume, then: $VA = (1/3) SA \times AE$ and $VB = (1/3) SB \times BG$. Let $n_A$ and $n_B$ be the number of faces of the polyhedra and assume $n_B > n_A$.
Ibn al-Haytham then shows that $BG > AE$ and therefore $VB > VA$. The proof consists in comparing $AE$ and $BG$ (fig. 23). We repeat it here to illustrate his method and style. Consider on $EC$ a point $K$ such that $GH = EK$, and on $ED$ a point $L$ such that $EL = GI$. If $AE = BG$, the pyramid $AEKL$ would be equal to pyramid $BGHI$, and the solid angle $(A, EKL)$ would equal the solid angle $(B, GHI)$. From Lemma 2 of Prop. 4 we know that
\begin{align} \frac{\text{solid angle}\ (A,\ ECD)}{4\pi}&=\frac{\text{pyramid}\ (AECD)}{V_A}= \notag \\ &=\frac{\text{area}\ (ECD)}{S_A} \end{align} \begin{align} \text{and:}\quad\frac{\text{solid angle}\ (B,\ GHI)}{4\pi}&=\frac{\text{pyramid}\ (BGHI)}{V_B}= \notag \\ &=\frac{\text{area}\ (GHI)}{S_B} \end{align}
Since $SA = SB$, it follows that:
\begin{equation} \frac{\text{area}\ (ECD)}{\text{area}\ (GHI)}=\frac{\text{solid angle}\ (A,\ ECD)}{\text{solid angle}\ (B,\ GHI)}\ \text{,} \end{equation}and thus also:
\begin{equation} \frac{\text{area}\ (ECD)}{\text{area}\ (GHI)}=\frac{\text{solid angle}\ (A,\ ECD)}{\text{solid angle}\ (A,\ EKL)}\ \text{,} \end{equation}which, by Lemma 8, is absurd. Therefore $AE \ne BG$. If $BG < AE$ (fig. 23c), there exists a point $M$ on $AE$ such that $EM = BG$, and the solid angle $(M, EKL)$ equals the solid angle $(B, GHI)$. But then we would have: $\angle EMK = \angle EAK, \angle EML = \angle EAL, \angle KML = \angle KAL$ (vertices of isosceles triangles with the same bases $KE, EL, KL$), from which:
\begin{equation} \widehat{EMK}+\widehat{EML}+\widehat{KML}>\widehat{EAK}+\widehat{EAL}+\widehat{KAL} \ \text{,} \end{equation}and thus the solid angle $(M, EKL)$ would be greater than the solid angle $(A, EKL)$. By Lemma 8:
\begin{equation} \frac{\text{area}\ (ECD)}{\text{area}\ (EKL)}=\frac{\text{solid angle}\ (A,\ ECD)}{\text{solid angle}\ (A,\ EKL)}\ \text{,} \end{equation}and hence:
\begin{equation} \frac{\text{area}\ (ECD)}{\text{area}\ (EKL)}=\frac{\text{solid angle}\ (A,\ ECD)}{\text{solid angle}\ (M,\ EKL)}\ \text{,} \end{equation}that is:
\begin{equation} \frac{\text{area}\ (ECD)}{\text{area}\ (BHI)}=\frac{\text{solid angle}\ (A,\ ECD)}{\text{solid angle}\ (B,\ GHI)}\ \text{,} \end{equation}which contradicts equation (96). Therefore, necessarily $BG > AE$, and consequently $VB > VA$.
To prove the second proposition, Ibn al-Haytham considers two regular polyhedra inscribed in the same sphere, with surface areas $S_1$ and $S_2$, volumes $V_1$ and $V_2$, and numbers of faces $n_1$ and $n_e$ such that $n_1> n_e$ . If $A$ is the center of the sphere circumscribed about both polyhedra, there will be n₁ identical regular pyramids with vertex $A$ associated with the faces of $P_1$, and n₂ identical regular pyramids associated with the faces of $P_2$.
Let $\alpha_1$, $s_1$, and $h_1$ be the vertex angle, base area, and height of a regular pyramid $P_1^{\prime}$ associated with $P_1$, and $\alpha_2$, $s_2$, and $h_2$ the corresponding elements of a pyramid $P_2^{\prime}$ associated with $P_2$. We have: $n_1\alpha_1 = n_2\alpha_2 = 4\pi$, and since $n_1 > n_2$, it follows that $\alpha_1 < \alpha_1$. We can assume the two pyramids $P_1^{\prime}$ and $P_2^{\prime}$ share the same axis $AH$; since $\alpha_1 < \alpha_2$, the solid angle of $P_1^{\prime}$ lies within that of $P_2^{\prime}$, and the edges of $P_1^{\prime}$ intersect the sphere beyond the base plane of $P_2^{\prime}$. The planes of the two bases are parallel and intersect the sphere along the circles circumscribed around the bases; it follows that $s_1 < s_2$ and $h_1 > h_2$. Furthermore:
\begin{equation} \frac{\alpha_1}{4\pi}=\frac{s_1}{S_i}=\frac{\ 1\ }{n_i}\quad\text{and}\quad \frac{\alpha_2}{4\pi}=\frac{s_2}{S_2}=\frac{\ 1\ }{n_2} \end{equation}from which:
\begin{equation} \frac{\alpha_2}{\alpha_1}=\frac{s_2}{S_2}\cdot\frac{S_1}{s_1}= \frac{s_2}{s_1}\cdot\frac{S_1}{S_2}\ \text{.} \end{equation}It was shown (Prop. 9) that $\alpha_2/\alpha_1 < s_2/s_1$, so $(s_2/s_1) \times (S_1/S_2) < s_2/s_1$, from which $S_1 < S_2$. We know that $V_1 = (1/3)S_1h_1$ and $V_2 = (1/3)S_2h_2$, and since $S_1 < S_2$ and $h_1 > h_2$, we get $V_1 > V_2$. This theorem, though generally provable using Ibn al-Haytham’s method, applies only to the tetrahedron, octahedron, and icosahedron.
He then proves the following corollary: let $P_1$ and $P_2$ be two regular polyhedra inscribed in the same sphere and having n₁ and n₂ faces, respectively, such that the faces are regular polygons with $n_1^{\prime}$ and $n_2^{\prime}$ sides; if $n_1 > n_2$ and $n_1^{\prime}> n_2^{\prime}$, then $S_1 > S_2$ and $V_1> V_2$. Since the polyhedra in question are regular, this corollary means that if a regular tetrahedron, cube, and dodecahedron are inscribed in the same sphere, their lateral surface areas and volumes increase in that order. We have seen that the dynamic procedure followed by Ibn al-Haytham to solve the isoperimetric problem in space – thought of somewhat analogously to that used in the plane – runs up against the fact that the number of regular polyhedra is finite.
This contribution by Ibn al-Haytham, and before him that of al-Hāzin, are by far the most significant in Arabic mathematics. To our knowledge, no one else equaled them. The research conducted by their successors – among them Ibn Hūd, Jābir ibn Aflah, and Abū ’l-Qāsim al-Sumaysāṭī – does not reach the level of that of al-Hāzin, and even less so that of Ibn al-Haytham. Ibn Hūd does examine the isoperimetric problem in his book al-Istikmāl (The Perfection), but he merely reproduces Ibn al-Haytham’s demonstration with some variations. As for al-Sumaysāṭī, he adds nothing essential to al-Hāzin’s results. Jābir ibn Aflah, the Andalusian astronomer, in his Iṣlāḥ al-Majisṭī (The Rectification of the Almagest), considers only the spatial case and limits his demonstrations to regular polyhedra.
It is very likely that from the Latin translation of the latter book, Thomas Bradwardine drew a proposition found in Book II of his Geometria speculativa – a proposition that would later be echoed by Cardano in De subtilitate – stating: among all isoperimetric planar figures having the same number of sides and equal angles, the largest is the one with equal sides. This corresponds exactly to Prop. 6 of al-Hāzin.
Only future historical research will tell us whether there were other studies on par with those of al-Hāzin and Ibn al-Haytham, whether the latter’s contribution was resumed and developed, and whether part of this topic was transmitted to Latin mathematicians. Without wishing to extinguish all hope, it nonetheless seems unlikely that anyone went beyond Ibn al-Haytham (his research on the solid angle will confirm this) without additional analytical tools – still yet to be invented. But this remains only a conjecture.
In the course of his research on the isoperimetric problem in space, Ibn al-Haytham developed a theory of the solid angle. This is the first true theory of the solid angle since that, rather modest, of Euclid, and it would not be matched, let alone surpassed, for many centuries. With it, in the 11th century, Archimedean research in geometry would gain a new chapter. To fully appreciate Ibn al-Haytham’s contribution, we must briefly retrace the history of studies on the solid angle before him.
The first work we know of is that of Euclid in the Elements. In Book XI, which begins the study of solid geometry, Euclid defines the solid angle and elaborates a theory in propositions 20, 21, 22, 23, and 26, before applying it in propositions 27, 36, and 37 of the same book, and in the scholium of Book XIII. This theory, it must be said, concerns less the solid angle itself than the relationships between the plane angles that compose it. Book XI includes 28 definitions. The eleventh, concerning the solid angle, is as follows: “A solid angle is the inclination [mutual] of more than two lines which meet one another but are not in the same surface. Or alternatively: a solid angle is that which is contained by more than two plane angles which are not in the same plane and which meet in a common point [vertex].”
It is clear that in this double definition, the first – of the plane angle – is modeled on Def. VIII of Book I (a plane angle is the mutual inclination of two straight lines meeting in a plane and not having the same direction). It is equally clear that, taken literally, this definition raises many problems. Consider a solid angle formed by the inclination of three curved lines: these, taken in pairs, do not form a plane angle because they are not coplanar. The second definition in turn seems to permit only one kind of solid angle. For example, it would not allow us to refer to the solid angle at the vertex of a cone of revolution. Be that as it may, this double definition has generated rivers of ink, and even the authenticity of the first definition has been doubted (Heath 1926). The second definition was adopted by the Arabic tradition of the Elements, in various copies of the translation by Isḥāq and Thābit, and it is this definition that Ibn al-Haytham reproduces in his Kitāb fī ḥall shukūk kitāb Uqlīdis fī al-Uṣūl (Book on the Resolution of Doubts about Euclid's Elements). However, we find the first definition in a fragment containing the prologue of Book XI, whose translation is explicitly attributed to Isḥāq’s father, Ḥunayn ibn Isḥāq (this fragment is interleaved over two folios in manuscript Malik 3586 preserved in Tehran).
The five propositions constituting Euclid’s theory of the solid angle are as follows. Prop. 20 states that if a solid angle is contained by three plane angles, the sum of any two of them, taken in any way, is greater than the remaining one. Prop. 21 states that every solid angle is contained by plane angles whose sum is less than four right angles. Regarding the latter, Thomas Heath rightly notes: “It will be observed that, although Euclid states the proposition for all solid angles, it is proved only in the special case of a trihedral angle” (1926, III, p. 210). Euclid’s proof depends on Prop. 32 of Book I and thus on the parallel postulate, and we know, after Nikolai I. Lobachevsky and Bolyai, that spherical geometry does not depend on the parallel postulate.
The statement of Prop. 22 is as follows: if there are three plane angles, and the sum of any two of them, taken in any way, is greater than the remaining one, and such angles are included between straight lines, it is possible to construct a triangle with the lines connecting the ends of the equal lines. This proposition is actually a lemma used to prove Prop. 23, which is the main one in this group: with three plane angles, such that the sum of any two of them is greater than the remaining one, construct a solid angle; it is therefore necessary that the sum of the three angles is less than four right angles. Finally, Prop. 26 reads: on a given straight line [as edge] and at a point on it [as vertex], construct a solid angle equal to a given solid angle.
Without having first defined the equality of two solid angles in terms of measurement, Euclid proves this final proposition by actually assuming that two trihedral angles are equal: “This proposition again assumes the equality of two trihedral angles that have the three plane angles of one respectively equal to the three plane angles of the other taken in the same order” (ibid., p. 329). In other words, Euclid assumes without proof that two trihedral solid angles are equal if the plane angles that form them are pairwise equal. This is an implicit hypothesis that, among other things, is not always true, as can be seen by considering a solid angle formed by four plane angles: it is possible in this case to form infinitely many different solid angles with the given four plane angles. Nevertheless, the statement of proposition 26 is true without restrictions. The discrepancy between the statement and the proof is telling: to the generality of the statement – Euclid does not specify the nature of the solid angle – corresponds a proof limited only to trihedral solid angles, indicating that in the Elements, Euclid deals solely with these. However, this is not the only limitation. We have seen that Euclid aims to establish the equality of two solid angles without explicitly defining the notion of equality. It follows that he tacitly assumes a solid angle to be a quantity just like others, such as the plane angle, for example. But he never provides any rules to treat this quantity, such as comparing solid angles using the right solid angle defined by three right plane angles. This comparison, even if limited to trihedra, is independent of the sum of the plane angles that define the solid angle. Thus, one would search in vain in the Elements for any study of the solid angle as a quantity: the theory of the solid angle remains extremely poor.
After Euclid, the history of the solid angle did not gain new contributions. The only information comes from the second part, devoted to solid bodies, of Book V of the Mathematical Collection. Pappus writes concerning the thirteen semiregular polyhedra:
“In fact, if for polyhedra whose solid angles are enclosed by three plane angles one simply counts the plane angles at the bases of the polyhedron, it is evident that the number of solid angles is one third of the number obtained; whereas for polyhedra where the solid angle is enclosed by four plane angles, if all the angles at the bases are counted, the number of solid angles of the polyhedron is one fourth of the resulting number. Finally, similarly for polyhedra where the solid angle is enclosed by five plane angles, the number expressing the quantity of solid angles is one fifth of the number of plane angles.” (I, p. 274)
This concerns, as Pappus reminds us, the thirteen polyhedra discovered by Archimedes in the now-lost book. Thus, after Euclid, the solid angle is at least recalled by Archimedes in his research on semiregular polyhedra. But since we do not know this work of the mathematician from Syracuse, what we know ends here. This, it seems, is the state of research on the solid angle up to its revival in the 9th century. The history of studies on the solid angle has not yet been written, but we can affirm that from that moment, research takes two directions. The first is based on Book XI of the Elements and aims to improve Euclid's proof; the second is directly related to the approximation of a convex body by polyhedra. As an example of works in the first direction, we cite those of al-Sijzī and Ibn al-Haytham, but there were probably others as well, while the second direction is followed by Ibn al-Haytham.
The first mathematician known to have taken an interest in the solid angle is, as far as we know, Aḥmad ibn ʿAbd al-Ḥalīl al-Sijzī (second half of the 10th century). He returns to the solid angle at least twice. In a book titled al-Madkhal ilā ʿilm al-handasa (Introduction to the Science of Geometry), he undertakes a classification of the different types of solid angles: “one is that enclosed by a single surface, the second by a surface and a plane, and the third by two planes” (Dublin, Chester Beatty, 3652, f. 8). The examples he provides are: for the first type, the angle at the vertex of a cone of revolution or one at a vertex of an ellipsoid; for the second, a semicone of revolution; for the third type, the angle enclosed by three planes – the trihedral – in which the sum is less than four right angles. In another work, Risāla fī ḥall al-shakk alladhī fī al-ḥukm al-ṣāliḥ wa-l-ʿādhirīn min al-maqāla al-ḥādiyya ʿashara min kitāb Uqlīdis (Treatise on the Clarification of the Doubt Regarding Prop. 23 of Book XI of Euclid), he revisits the lemma and proposition of Euclid. In the introduction, he addresses other mathematicians who had raised doubts about Euclid’s proof. This indicates that al-Sijzī was not the only one at the time concerned with the solid angle, at least within the Euclidean framework.
The second mathematician is Ibn al-Haytham himself. He also revisits Euclid’s proof in order to correct it in his Kitāb fī ḥall shukūk Kitāb Uqlīdis fī al-Uṣūl. These studies, interesting both for the history of Book XI of the Elements in Arabic and for that of the solid angle, do not, however, radically change the nature of Euclid’s theory.
The third study, by far the most innovative and important, is that of Ibn al-Haytham in his book on isoperimetric figures in the plane and in space. It is in this text that he develops a theory of the solid angle. How did he arrive at this theory? As we have seen, one of the goals he sets himself is to demonstrate the maximal property of the sphere. Following his predecessors, such as al-Ḥasan ibn al-Haytham, he
adopts an infinitesimal strategy – that is, a procedure that consists in approximating the volume of the sphere by a sequence of volumes of convex polyhedra. The unfortunate choice of regular polyhedra does not change the underlying intention of this strategy, which nevertheless requires that one be able to compare the volumes of convex polyhedra. Now, such a comparison is evidently simpler if one proceeds through the solid angle, and consequently if one compares solid angles. But comparison can only be made between magnitudes, and by means of magnitudes. It was therefore necessary to explicitly conceive the solid angle as a magnitude, and thus subject to the operations applicable to magnitudes and the theory of proportions. He then establishes numerous lemmas on the solid angle: the aim is to demonstrate the extremal property, but these lemmas constitute the theorems of a new theory of the solid angle. What method did he follow to establish this theory?
In such a situation, the most natural – albeit not easy – path is that of analogy: starting from the theory of the plane angle and generalizing it to space. But one must not be misled: this analogy is, at most, heuristic in value; the transition to space is not simple and presents many pitfalls. Indeed, many properties that hold in the case of the plane angle no longer apply to the solid angle. Knowledge of the relationships between chords and the central angles they subtend on the circumference would provide Ibn al-Haytham with some remarkable insights, but nothing concerning the conceptual framework of the theory of the solid angle. He therefore finds himself in a situation unlike any other, as he places himself, so to speak, within the perspective of Archimedean geometry using the tools of spherical geometry; we are far removed from the Euclidean framework. To illustrate this, let us consider the elements of this theory.
Ibn al-Haytham begins by recalling a result of Archimedes, which he proves anew in the treatise Qawl fī misāḥat al-kura: the volume of the sphere of radius $r$ is $\frac{4}{3} \pi r^3$. Ibn al-Haytham then writes:
“Every regular polyhedron inscribed in the sphere is such that, if planes are drawn from the center of the sphere passing through the sides of one of its bases, these planes divide from the sphere a sector whose ratio to the whole sphere is equal to the ratio between the spherical surface base of the sector and the total surface of the sphere, and is equal to the ratio between the solid angle – which is located at the center of the sphere and bounded by the surfaces of the regular pyramid whose lines are straight and whose base is one of the bases of the polyhedron – and the eight right solid angles that are the sum of all the solid angles at the center of the sphere and that are at the center of all regular polyhedra insofar as the sphere and its surface are divided by these planes into equal parts.” (Rashed 1993a, pp. 401-402)
In this passage, he introduces the notion of solid angle in its relationship with spherical surfaces and spherical sections. More precisely, if $A$ is the area of the sphere, $s$ the area of the spherical surface of the section, $v$ the volume of the spherical section, $V$ the volume of the sphere, $\alpha$ the solid angle, $D$ the right solid angle, we have:
\begin{equation} \frac{v}{V}=\frac{\ s\ }{A}= \frac{\alpha}{8D} \end{equation}and the ratios are equal to $n$, where $n$ is the number of faces of the polyhedron. Only afterward does he define and construct the right solid angle:
“If one takes a great circle of the sphere, draws two diameters that intersect at a right angle, draws from the center a perpendicular to the plane of the circle and extends it in both directions, then draws from the two ends of this perpendicular lines [also perpendicular] to the ends of the two diameters, eight equal pyramids are formed in the sphere with vertices at the center of the sphere and equal vertex angles. Each of these angles is called a ‘right solid angle’, and the sum of these angles is the sum of the angles of any polyhedron inscribed in the sphere.” (ibid., p. 402)
He then deduces that $v = \frac{\ 1\ }{3}sr$. It is already clear here that he does not opt for Euclid’s definition of the solid angle. Instead, he begins with a regular polyhedron inscribed in a sphere. To each face of the polyhedron, he associates a regular pyramid whose vertex is the center $B$ of the sphere. Using [104], he defines a solid angle with vertex $B$, a spherical surface, and a section of the sphere. He then demonstrates six propositions. Proposition 1 is as follows. Let $A$ be the center of a sphere (fig. 24), and consider two pyramids $P_1(ABCDE)$ and $P_2(AHFG)$. Pyramid $P_1$, with solid angle $\alpha_1$, intercepts a spherical surface $s_1$ and bounds a spherical section of volume $v_1$. Similarly, $P_2$ corresponds to $\alpha_2$, $s_2$, and $v_2$. One has:
\begin{equation} \frac{\alpha_1}{\alpha_2}=\frac{s_1}{s_2}= \frac{v_1}{v_2} \end{equation}If $n$ copies of pyramid $P_1$ are considered, then the part of the sphere associated is of volume $nv_1$, the intercepted spherical surface is $ns_1$, and the solid angle is $n\alpha_1$, and the same holds for $P_2$.
• If $nv_1 > nv_2$, then $n\alpha_1 > n\alpha_2$ and $ns_1 > ns_2$ ;
• if $nv_1 < nv_2$, then $n\alpha_1 < n\alpha_2$ and $ns_1 < ns_2$ ;
• if $nv_1 = nv_2$, then $n\alpha_1 = n\alpha_2$ and $ns_1 = ns_2$ ;
• if $n\alpha_1 > n\alpha_2$, then $ns_1 > ns_2$ and $nv_1 > nv_2$ ;
• if $n\alpha_1 < n\alpha_2$, then $ns_1 < ns_2$ and $nv_1 < nv_2$ ;
• if $n\alpha_1 = n\alpha_2$, then $ns_1 = ns_2$ and $nv_1 = nv_2$ .
It should be noted that the explanations given by Ibn al-Haytham do not constitute a proof of the stated property (105). Proposition 2 states that, if $ABCD$ is a pyramid such that $\angle ABC = \pi /2$ and $\angle ABD = \pi /2$, and if $E$ is a point on $BD$ such that $\angle AEC = \pi /2$ or $\angle ACE = \pi /2$, then:
\begin{equation} \frac{\text{area}\ (DBC)}{\text{area}\ (ECB)}=\frac{\text{solid angle}\ (A,\ BDC)}{\text{solid angle}\ (A,\ EBC)}\ \text{,} \end{equation}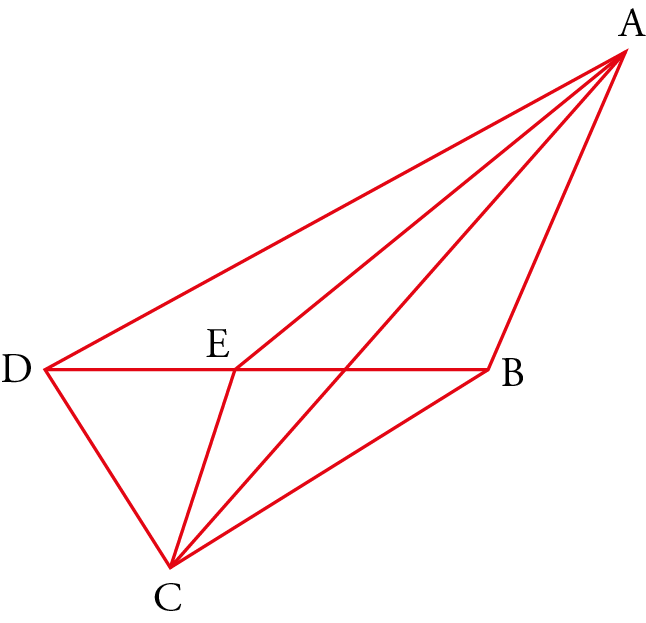
Let $\Sigma$ be a sphere centered at $A$ with radius $AB$, intersecting $AC$ at $H$, $AD$ at $I$, and $AE$ at $L$, such that $AB = AH = AI = AL$. Then, in the plane $(BAC)$ is arc $BH$, in $(BAD)$ arc $BLI$, in $(ACD)$ arc $HI$, and in $(ACE)$ arc $HGL$. The line $BL$ lies in plane $(BAD)$, intersects $AD$ at $K$ (since $\angle ABL$ is acute, and so is $\angle BAD$). Arc $LGH$ lies on $\Sigma$, and thus $K$ lies outside $\Sigma$, with $AK > AI$. The conic surface from vertex $B$ defined by arc $LGH$ intersects plane $(ADC)$ along arc $KFH$, as each line $BG$ intersects this plane at $F$ outside the sphere $\Sigma$; arc $KFH$, excluding $H$, lies outside $\Sigma$. Then the spherical section $AILGH$ lies within the solid $AKFHGL$, bounded by planes and part of the conic surface, since generator segment $GF$ lies outside $\Sigma$ and spherical section $ALHB$ is larger than the solid $ALHB$, bounded by planes and another part of the conic surface, since cone generator $BG$ lies within $\Sigma$.
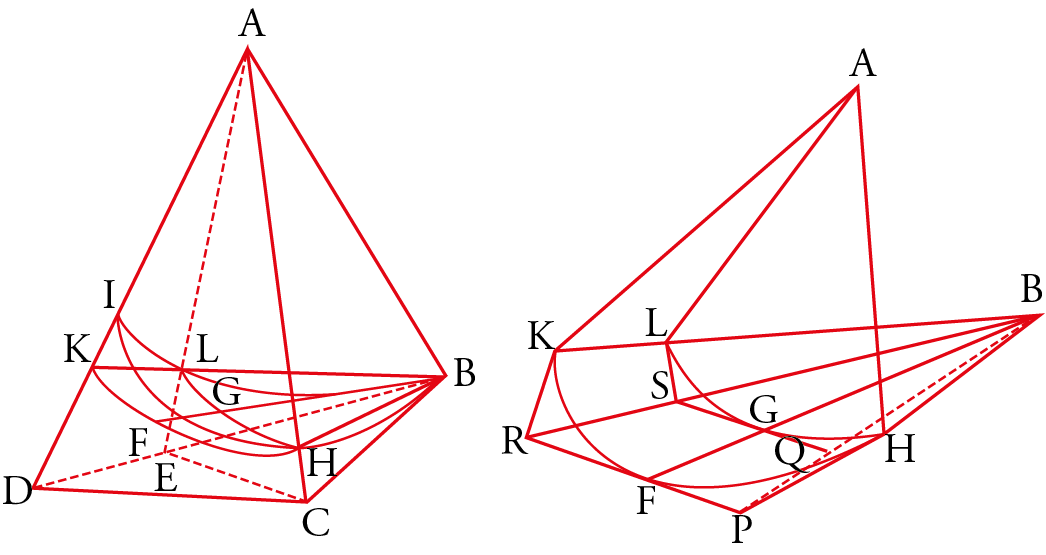
By composition:
\begin{equation} \frac{\text{sector}\ (A,\ IHB)}{\text{sector}\ (A,\ LHB)}<\frac{\text{solid}\ (B,\ AKFH)}{\text{solid}\ (B,\ AHGL)}\ \text{.} \end{equation}During the proof of this Prop. 2, Ibn al-Haytham introduces another proposition with the statement:
\begin{equation} \frac{\text{area}\ (AEC)}{\text{sector area}\ (ALGH)}\ge\frac{\text{area}\ (ADC}{\text{sector area}\ (AKFH)}\ \text{;} \end{equation}in other words, he aims to demonstrate that the conic projection from vertex $B$ of plane $AEC$ onto plane $ADC$ increases some area ratios starred with respect to $A$. The proof involves a reductio ad absurdum, reducing to comparing areas of triangles with vertex $A$. Let’s follow the steps of this demonstration. Suppose:
\begin{equation} \frac{\text{area}\ (AEC)}{\text{sector area}\ (ALGH)}>\frac{\text{area}\ (ADC}{\text{sector area}\ (AKFH)}\ \text{;} \end{equation}there exists an area $L_a$ (fourth proportional) such that:
\begin{equation} \frac{\text{area}\ (AEC)}{L_a}=\frac{\text{area}\ (ADC}{\text{sector area}\ (AKFH)}\ \text{.} \end{equation}The hypothesis is then written as $L_a > \text{sector area}(ALGH)$, and thus there exists a polygon $LSQH$ circumscribed around arc $LGH$ such that:
\begin{equation} \operatorname{area}(ALSQH) < L_a \ \text{.} \end{equation}He considers the case where this polygon has three sides – $LS, SQ, QH$ – tangent to the arc of a circle at points $L$, $G$, and $H$, respectively. The polygon $LSQH$ is projected onto plane $ADC$ as the polygon $KRPH$, whose sides $KR$, $RP$, and $PH$ are tangent at $K$, $F$, and $H$, respectively, to the projection $KFH$ (a conic arc) of the circular arc $LGH$.
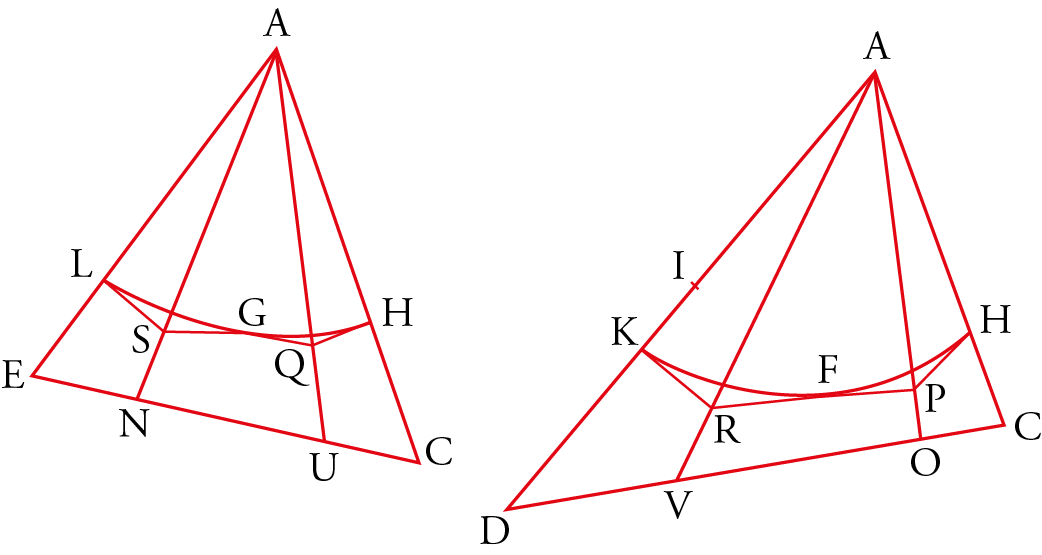
It is worth noting that Ibn al-Haytham is perfectly aware that conic projection preserves tangency, which recalls the properties of the tangent plane to the cone known to Ibn Sahl. The statement is thus reduced to the inequality:
\begin{equation} \frac{\text{area}\ (ADC)}{\text{area}\ (AKRPH)}>\frac{\text{area}\ (AEC}{\text{area}\ (ALSQH)}\ \text{.} \end{equation}In fact, the second ratio in (113) is, according to (112), greater than the ratio:
\begin{equation} \frac{\text{area}\ (AEC)}{L_a}=\frac{\text{area}\ (ADC}{\text{area}\ (AKFH)}\ \text{,} \end{equation}and so from (111) it follows that:
\begin{equation} \text{area}\ (AKRPH)<\text{sector area}\ (AKFH)\ \text{,} \end{equation}which is absurd, because the polygon is circumscribed around the arc. Ibn al-Haytham then states that inequality (113) results from the inequalities:
\begin{align} \frac{\text{area}\ (AEN)}{\text{area}\ (ALS)}&<\frac{\text{area}\ (ADV)}{\text{area}\ (AKR)}\ ; \notag \\ \frac{\text{area}\ (ANU)}{\text{area}\ (ASQ)}&<\frac{\text{area}\ (AVO)}{\text{area}\ (ARP)}\ ; \notag \\ \frac{\text{area}\ (AUC)}{\text{area}\ (AQH)}&<\frac{\text{area}\ (AOC)}{\text{area}\ (APH)} \ \text{.} \end{align}Unfortunately, this last assertion is not always true. However, the proposition holds when points $C$ and $D$ lie on the same side of the plane perpendicular to $ABD$ and passing through $AB$ – a condition missed by Ibn al-Haytham but which does not invalidate the subsequent propositions depending on it. Ibn al-Haytham always places himself in favorable conditions.
Proposition 3 states that, given a pyramid $ABCD$ such that $AB$ is perpendicular to plane $(BCD)$ and angle $\angle BCD = \pi /2$, if $E$ is a point on $CD$, then:
\begin{equation} \frac{\text{area}\ (DBC)}{\text{area}\ (EBC)}<\frac{\text{solid angle}\ (A,\ BDC)}{\text{solid angle}\ (A,\ EBC)}\ \text{.} \end{equation}In plane $ABE$, draw the perpendicular from $E$ to $AE$. It intersects $AB$ at $G$. Since $\angle BCE = \pi /2$, $BE \perp BC$, and since $AB\perp \text{plane} (BCD)$, then $AE \perp AC$. Extend $BC$ to $E^{\prime}$ such that $BE^{\prime} = BE$, so $\angle AE^{\prime}G = \angle AEG = \pi /2$, hence $\angle ACG$ is obtuse.
Let’s prove $\angle ACD = \pi /2$. If $\angle BCD = \pi /2$, then $CB \perp CD$; since $CD \perp AB$, it follows $CD \perp \text{plane} (ABC)$, and thus $CD \perp AC$, that is $\angle ACD = \pi /2$. If $\angle BCD < \pi /2$, we can draw $CD^{\prime}$ inside angle $BCD$ such that $CD^{\prime} \perp BC$, hence $CD^{\prime} \perp \text{plane} (ABC)$, and $AC \perp CD^{\prime}$, so $\angle ACD^{\prime} = \pi /2$ and $D^{\prime}$ is inside $BD$.
In plane $ACG$, draw $CG^{\prime}$ perpendicular to $AC$ with $G^{\prime}$ on $BG$. Then the plane $CD^{\prime}G^{\prime}$ is perpendicular to $AC$ and intersects plane $ABD$ along line $G^{\prime}D^{\prime}$, which meets $AD$ between $A$ and $D$ at $D^{\prime\prime}$, and we have $2\angle AC D^{\prime\prime} = \pi /2$, hence $\angle ACD < \pi /2$. Then pyramid $AGCD$ satisfies the conditions of Prop. 2. If $\angle AEG$ is right, we have seen the proposition is not always true, but the lemma remains valid.
Ibn al-Haytham continues:
\begin{equation} \frac{\text{area}\ (GCD)}{\text{area}\ (GCE)}>\frac{\text{solid angle}\ (A,\ GCD)}{\text{solid angle}\ (A,\ GCE)}\ \text{.} \end{equation}but:
\begin{equation} \frac{\text{area}\ (GCD)}{\text{area}\ (GCE)}=\frac{CD}{CE}=\frac{\text{area}\ (DBC)}{\text{area}\ (EBC)}\ \text{;} \end{equation}Moreover, solid angle $(A, GCD) = \text{solid angle} (A, BCD)$ and solid angle $(A, GCE) = \text{solid angle} (A, BCE)$, hence the result:
\begin{equation} \frac{\text{area}\ (DBC)}{\text{area}\ (EBC)}>\frac{\text{solid angle}\ (A,\ BDC)}{\text{solid angle}\ (A,\ BCE)}\ \text{.} \end{equation}Proposition 4 states that, given a pyramid $ABCD$ where $AB \perp \text{plane} (CBD)$ and $BC = BD$; if $EG$ is parallel to $CD$, then:
\begin{equation} \frac{\text{area}\ (CDB)}{\text{area}\ (EBG)}>\frac{\text{solid angle}\ (A,\ BCD)}{\text{solid angle}\ (A,\ BEG)}\ \text{.} \end{equation}
Since $EG$ is parallel to $CD$, triangle $BGE$ is isosceles. If $I$ is the midpoint of $EG$, then $BI \perp EG$ and intersects $DC$ at $H$, the midpoint of $CD$. Now, from $AB \perp (CBD)$ follows that $(ABC) \perp (CBD)$ and $(ABH) \perp (CBD)$. Since $BH$ is the intersection of $(ABH)$ and $(BCD)$, and line $GI$ in $(BCD) \perp BH$, it is perpendicular to plane $(ABH)$, hence $\angle AIG = \pi /2$, and similarly $\angle AHC = \pi /2$.
We know that $\angle AIH$ and $\angle AIC$ are obtuse and that $\angle BHC = \pi /2$; we can apply Prop. 2 with the obtuse angle $\angle AIC$; it is again the borderline case, yet remains valid because points $C$ and $H$ are on the same side of the plane perpendicular to $ABH$ passing through $AB$ ($CH$ is parallel to this plane):
\begin{equation} \frac{\text{area}\ (BCH)}{\text{area}\ (BCI)}>\frac{\text{solid angle}\ (A,\ BCH)}{\text{solid angle}\ (A,\ BCI)}\ \text{.} \end{equation}The same Prop. 2, with the right angle $\angle AIG$ (true in all cases; this angle $\angle AIG$ plays the role of $\angle ACE$ in Prop. 2), gives:
\begin{equation} \frac{\text{area}\ (CBI)}{\text{area}\ (IBG)}>\frac{\text{solid angle}\ (A,\ BCI)}{\text{solid angle}\ (A,\ BIG)}\ \text{.} \end{equation}Multiplying term by term yields:
\begin{equation} \frac{\text{area}\ (HBC)}{\text{area}\ (IBG)}>\frac{\text{solid angle}\ (A,\ BCH)}{\text{solid angle}\ (A,\ BIG)}\ \text{.} \end{equation}From this, multiplying both terms of the ratio by 2, we deduce:
\begin{equation} \frac{\text{area}\ (DBG)}{\text{area}\ (BEG)}>\frac{\text{solid angle}\ (A,\ BCD)}{\text{solid angle}\ (A,\ BEG)}\ \text{;} \end{equation}a direct integral calculation could also demonstrate this lemma independently of Prop. 2.
Prop. 5 concerns two regular pyramids $P_1$ and $P_2$ with vertex $A$, whose bases are similar but different regular polygons inscribed in a sphere centered at $A$. Let $P_1$ be the pyramid with the larger base and $P_2$ the other pyramid; then:
\begin{equation} \frac{\text{solid angle}\ A\ \text{of}\ P_1}{\text{solid angle}\ A\ \text{of}\ P_2}>\frac{\text{base of}\ P_1}{\text{base of}\ P_2}\ \text{.} \end{equation}The fundamental idea of the proof, here as elsewhere, is to take the area of the spherical surface intercepted by the solid angle as its measure.
Finally, according to Prop. 6, given two regular pyramids $P_1$ and $P_2$ with vertex $A$, having respectively n₁ and n₂ faces and bases $B_1$ and $B_2$ inscribed in the same sphere centered at $A$ and with areas $s_1$ and $s_2$, if $n_1 > n_2$ and $s_1 < s_2$, then:
\begin{equation} \frac{\text{solid angle}\ A \ \text{of}\ P_2}{\text{solid angle}\ A\ \text{of}\ P_1}>\frac{s_1}{s_2}\ \text{.} \end{equation}These are the elements with which Ibn al-Haytham constructs a theory of the solid angle. As we have seen, the unifying principles of this theory are the notion that the solid angle is a magnitude just like other geometric magnitudes, and that this magnitude can be measured by the area of the spherical surface it intercepts. This allows for the definition of ratios between planar polygons inscribed in a sphere and solid angles at the center that intercept these polygons. At this point, the analogy with the theory of the plane angle no longer holds.
Examining the demonstrations of the preceding properties shows that Ibn al-Haytham combines conic projections with infinitesimal methods. This is thus one of the most advanced and sophisticated chapters of the time. It seems that developments in this area halted for six centuries, until the appearance of Descartes’ Progymnasmata de solidorum elementis and Florimond de Beaune’s La doctrine de l’angle solide. The latter follows his own path, while Descartes handles notions close to those of Ibn al-Haytham. Only with Euler and the abbé de Gua would the theory evolve through the application of differential and integral calculus.
Roshdi Rashed
- Becker 1936: Becker, Oskar, Zur Textgestaltung des eudemischen Berichts über die Quadratur der Möndchen durch Hippokrates von Chios, “Quellen und Studien zur Geschichte der Mathematik”, 3, 1936, pp. 400–419.
- – 1964: Becker, Oskar, Grundlagen der Mathematik, Freiburg-München, Alber, 1964.
- Clagett 1964–84: Archimedes in the Middle Ages, ed. by Marshall Clagett, v. I: The Arabo-Latin tradition, Madison, University of Wisconsin Press, 1964; v. V: Quasi-archimedean geometry in the thirteenth century, Philadelphia, American Philosophical Society, 1984.
- Coolidge 1940: Coolidge, Julian L., History of geometrical methods, Oxford, Oxford University Press, 1940 (repr. New York, Dover, 1963).
- Heath 1926: Heath, Thomas L., The thirteen books of Euclid’s Elements, 2nd ed., Cambridge, Cambridge University Press, 1926, 3 vols. (repr. New York, Dover, 1956).
- Mogenet 1961: Mogenet, Joseph, L’histoire des isopérimètres chez les Grecs, “Scrinium lovaniense. Mélanges historiques”, 24, 1961, pp. 69–78.
- Rashed 1991: Rashed, Roshdi, L’analyse et la synthèse selon Ibn al-Haytham, in: Mathématiques et philosophie de l’antiquité à l’âge classique. Hommage à Jules Vuillemin, dir. R. Rashed, Paris, CNRS, 1991, pp. 131–162. (Eng. trans. in: Artifacts, representations and social practice, ed. C.C. Gould and R.S. Cohen, Dordrecht, Kluwer, 1994, pp. 121–140).
- – 1993a: Rashed, Roshdi, Math. inf. II.
- – 1993b: Rashed, Roshdi, Al-Kindi’s commentary on Archimedes’ ‘The measurement of the circle’, “Arabic Sciences and Philosophy”, 3, 1993, pp. 7–53.
- – 1993c: Rashed, Roshdi, Géométrie et dioptrique: Ibn Sahl, al-Qùhê et Ibn al-Haytham, Paris, Les Belles Lettres, 1993.
- – 1996a: Rashed, Roshdi, Math. inf. I.
- – 1996b: Rashed, Roshdi, Archimedean learning in the Middle Ages: the Banū Mūsā, “Historia Scientiarium”, 6, 1996, 1, pp. 1–16.
- – 2000a: Rashed, Roshdi – Bellosta, Hélène, Ibrāhīm ibn Sinān. Logique et géométrie au Xe siècle, Leiden, E.J. Brill, 2000.
- – 2000b: Rashed, Roshdi, Math. inf. III.
- – 2002: Rashed, Roshdi, Math. inf. IV.
- Rome 1936: Commentaires de Pappus et de Théon d’Alexandrie sur l’Almageste, éd. A. Rome, Roma, Biblioteca Apostolica Vaticana, 1931–1943, 3 vols.; v. II, 1936.
- Schmidt 1901: Schmidt, Wilhelm von, Zur Geschichte der Isoperimetrie im Altertume, “Bibliotheca Mathematica”, 2, 1901, pp. 5–8.
- Suter 1899: Suter, Heinrich, Die Kreisquadratur des Ibn al-Haitam, “Zeitschrift für Mathematik und Physik. Historisch-literarische Abteilung”, 44, 1899, pp. 33–47.
- Youschkevitch 1976: Youschkevitch, Adolf P., Les mathématiques arabes (VIIIe–XVe siècles), trad. fr. de M. Cazenave et K. Jaouiche, préface de R. Taton, Paris, Vrin, 1976.